题目内容
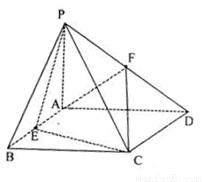
(本小题满分14分)如图,四棱锥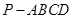 中,
中,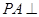 平面
平面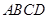 ,四边形
,四边形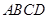 是矩形,
是矩形,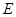 ,
,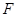 分别是
分别是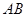 ,
,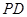 的中点.若
的中点.若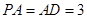 ,
,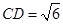 。
。
(1)求证: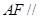 平面
平面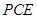 ;
;
(2)求直线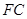 平面
平面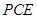 所成角的正弦值。
所成角的正弦值。
【答案】
(1)取PC的中点G,证明四边形AEGF是平行四边形,从而得证

(2)
【解析】
试题分析:(1)取PC的中点G,连结EG,FG,
又由F为PD中点,则 F G 
 . ……2分
. ……2分
|
|
又由已知有
∴四边形AEGF是平行四边形. ……4分
……4分
又AF 平面PEC, EG
平面PEC, EG
 . ……6分
. ……6分

(2)












故 ……10分
……10分 ……12分
……12分

 ,
,
 直线FC与平面PCE所成角的正弦值为
直线FC与平面PCE所成角的正弦值为 . ……14分
. ……14分
考点:本小题主要考查线面平行的证明,线面角的求解.
点评:解决立体几何问题,要充分发挥空间想象能力,更要紧扣判定定理和性质定理,定理中要求的条件要一一列举出来,求线面角时,要先作再证再求,还要注意线面角的取值范围.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)