题目内容
4.将函数y=cos2x的图象向右平移$\frac{π}{12}$个单位长度,所得图象的函数解析式为( )| A. | y=cos(2x+$\frac{π}{6}$) | B. | y=cos(2x+$\frac{π}{3}$) | C. | y=cos(2x-$\frac{π}{6}$) | D. | y=cos(2x-$\frac{π}{3}$) |
分析 将函数y=cos2x的图象向右平移$\frac{π}{12}$个单位,得到的新函数的解析式要在x上减去平移的大小,即可得解.
解答 解:将函数y=cos2x的图象向右平移$\frac{π}{12}$个单位,所得图象的函数解析式为y=cos[2(x-$\frac{π}{12}$)]=cos(2x-$\frac{π}{6}$).
故选:C.
点评 本题考查三角函数图象的平移的应用,本题解题的关键是抓住平移的方向和大小,注意这种情况下只在自变量的系数是1的情况下加或减,属于基础题.

练习册系列答案
相关题目
15.已知向量$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(1,-2),则$\overrightarrow{a}$•$\overrightarrow{b}$的值为( )
| A. | -4 | B. | 8 | C. | -1 | D. | -7 |
19.执行如图所示的程序框图,当输入x为16时,输出的y=( )
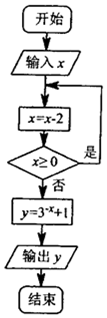

| A. | 28 | B. | 10 | C. | 4 | D. | 2 |
9.已知圆M的半径为1,若此圆同时与x轴和直线y=$\sqrt{3}$x相切,则圆M的标准方程可能是( )
| A. | (x-$\sqrt{3}$)2+(y-1)2=1 | B. | (x-1)2+(y-$\sqrt{3}$)2=1 | C. | (x-1)2+(y+$\sqrt{3}$)2=1 | D. | (x-$\sqrt{3}$)2+(y+1)2=1 |
13.函数f(x)=log2x+x-2的零点所在区间为[m,m+1](m∈Z),则m的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
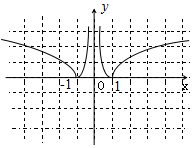 已知函数f(x)是定义在{x|x≠0}上的偶函数,且当x>0时,f(x)=log2x.
已知函数f(x)是定义在{x|x≠0}上的偶函数,且当x>0时,f(x)=log2x.