题目内容
【题目】在平面直角坐标系xOy中,已知直线l的普通方程为x﹣y﹣2=0,曲线C的参数方程为 ![]() (θ为参数),设直线l与曲线C交于A,B两点.若点P在曲线C上运动,当△PAB的面积最大时,求点P的坐标及△PAB的最大面积.
(θ为参数),设直线l与曲线C交于A,B两点.若点P在曲线C上运动,当△PAB的面积最大时,求点P的坐标及△PAB的最大面积.
【答案】解:∵曲线C的参数方程为 ![]() (θ为参数),
(θ为参数),
∴曲线C的普通方程为 ![]() =1,
=1,
联立 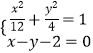 ,解得
,解得 ![]() 或
或 ![]() ,
,
∴A(0,﹣2),B(3,1),∴|AB|= ![]() =3
=3 ![]() ,
,
△PAB的面积最大,即点P到直线l的距离d最大,
设P( ![]() ,sinθ),则d=
,sinθ),则d= ![]() =
= ![]() ,
,
当cos( ![]() )=﹣1,即
)=﹣1,即 ![]() ,k∈Z时,
,k∈Z时,
![]() =3
=3 ![]() ,
,
∴△PAB的最大面积S= ![]() =
= ![]() =9.
=9.
此时P(﹣3, ![]() ).
).
【解析】先将曲线C的参数方程化为普通方程,联立曲线C的方程和直线l的方程可解得A,B的坐标,进而可得|AB|,再设P的坐标,计算点P到直线l的距离d,利用辅助角公式和三角函数的性质可得d的最大值,从而可得△PAB的最大面积及点P的坐标.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目