Question

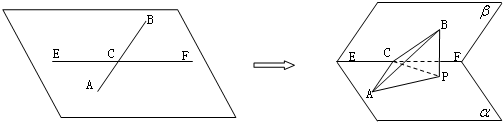
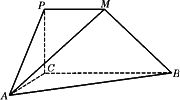
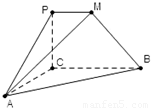
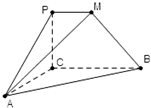如图，二面角P-CB-A为直二面角，∠PCB=90°，∠ACB=90°，PM∥BC，直线AM与直线PC所成的角为60°，又AC=1，BC=2，PM=1．
（1）求证：AC⊥BM；
（2）求二面角M-AB-C的正切值．

Answer 1

分析：（1）由已知二面角P-CB-A为直二面角，且∠ACB=90°，由面面垂直的性质得到ACAC⊥平面PCBM，进一步得到AC⊥BM；
（2）以C为坐标原点，建立空间直角坐标系，设出P点坐标，由直线AM与直线PC所成的角为60°求出P点坐标，然后求出平面MAB的一个法向量，找出平面ABC的一个法向量，由法向量所成角的余弦值得到二面角的余弦值，结合同角三角函数基本关系式求得二面角M-AB-C的正切值．

解答：（1）证明：∵平面PCBM⊥平面ABC，AC⊥BC，AC?平面ABC，
平面ABC∩平面PCBM=BC，∴AC⊥平面PCBM，
∵BM?平面PCBM，∴AC⊥BM；
（2）以C为坐标原点，以CA，CB，CP所在直线分别为x，y，z轴建立空间直角坐标系C-xyz，
如图，设P（0，0，z），（z＞0），
则B（0，2，0），A（1，0，0），M（0，1，z）．

AM

=(-1，1，z)，

CP

=(0，0，z)．
由直线AM与PC所成的角为60°，得

AM

•

CP

=|

AM

||

CP

|cos60°
即z2=

z2+2

•z•

1

2

，
解得z=

6

3

．
∴

AM

=(-1，1，

6

3

)，

AB

=(-1，2，0)，设平面MAB的一个法向量为

n1

=(x，y，z)．
由

n1 • AM =0 n1 • AB =0

，得

-x+y+ 6 3 z=0 -x+2y=0

，取y=2，得x=4，z=

6

．
求得

n1

=(4，2，

6

)，取平面ABC的一个法向量

n2

=（0，0，1）
则cos＜

n1

，

n2

＞=

n1 • n2

| n1 |•| n2 |

=

6

42+22+( 6 )2 •1

=

39

13

，
由图知二面角为锐二面角，所以二面角的正弦值为

1-( 39 13 )2

=

130

13

．
故二面角M-AB-C的正切值为

130 13

39 13

=

30

3

．

点评：本题考查了直线和平面垂直的判定，考查了平面和平面垂直的性质，考查了学生的空间想象能力和思维能力，训练了利用向量法求二面角的大小，解答的关键是建立正确的空间右手系，是中档题．