题目内容
已知数列{an}是首项为a且公比q不等于1的等比数列,Sn是其前n项和,a1,2a7,3a4成等差数列.
(Ⅰ) 证明12S3,S6,S12-S6成等比数列;
(Ⅱ)求和Tn=a1+2a4+3a7+…+na3n-2.
(Ⅰ)证明:由a1,2a7,3a4成等差数列.得4a7=a1+3a4,即4aq6=a+3aq3.变形得(4q3+1)(q3-1)=0,所以q3=- 或q3=1(舍去)由
或q3=1(舍去)由
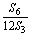 =
=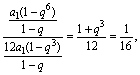
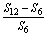 =
=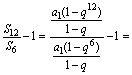 1+q6-1=q6=
1+q6-1=q6=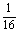 ,
,
得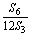 =
=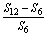 .所以12S3,S6,S12-S6成
.所以12S3,S6,S12-S6成 等比数列.
等比数列.
(Ⅱ)解法
:Tn=a1+2a4+3a7+…+na3a-2=a+2aq3+3aq6+…+naq3(n-2),
即Tn=a+2·(- )a+3·(-
)a+3·(- )2a+…+n·(-
)2a+…+n·(- )n-1a. ①
)n-1a. ①
①×(- )3a得:-
)3a得:- Tn=-
Tn=- a+2·(-
a+2·(- )2a+3·(-
)2a+3·(- )3a+…+n·(-
)3a+…+n·(- )na ②
)na ②
①-②有: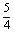 Tn=a+(-
Tn=a+(- )a+(-
)a+(- )2a+(-
)2a+(- )3a+…(-
)3a+…(- )n-1a-n·(-
)n-1a-n·(- )na=
)na=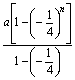 -n·(-
-n·(- )na=
)na=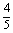 a-(
a-(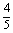 +n)·(-
+n)·(- )na.所以Tn=
)na.所以Tn=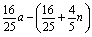 ·(-
·(- )na.
)na.

练习册系列答案
相关题目
 是奇函数,则实数
是奇函数,则实数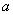 的值为 .
的值为 . 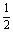 )内恒有f(x)>0,则f(x)的单调递增区间为 ( )
)内恒有f(x)>0,则f(x)的单调递增区间为 ( )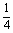 ) B.(-
) B.(-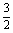 ,公差d=1,求满足Sk2=(Sk)2的正整数k;
,公差d=1,求满足Sk2=(Sk)2的正整数k; B.
B. C.
C. D.
D.

 的一条渐近线与抛物线
的一条渐近线与抛物线 只有一个公共点,且该双曲线的一个焦点为F(c,0)则
只有一个公共点,且该双曲线的一个焦点为F(c,0)则
 。
。