题目内容
设抛物线C: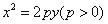 的准线被圆O:
的准线被圆O: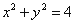 所截得的弦长为
所截得的弦长为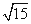 ,
,
(1)求抛物线C的方程;
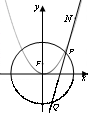
(2)设点F是抛物线C的焦点,N为抛物线C上的一动点,过N作抛物线C的切线交圆O于P、Q两点,求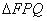 面积的最大值.
面积的最大值.
(1)因为抛物线C的准线方程为 ,且直线
,且直线 被圆O:
被圆O: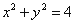 所截得的弦长为
所截得的弦长为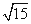 ,所以
,所以 ,解得
,解得 ,因此抛物线C的方程为
,因此抛物线C的方程为 ;(4分)
;(4分)
(2)设N( ),由于
),由于 知直线PQ的方程为:
知直线PQ的方程为: . 即
. 即 .
.
(6分)
因为圆心O到直线PQ的距离为 ,所以|PQ|=
,所以|PQ|= ,(7分)
,(7分)
设点F到直线PQ的距离为d,则 ,( 8分)
,( 8分)
所以,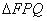 的面积S
的面积S



 (11分)
(11分)
当 时取到“=”,经检验此时直线PQ与圆O相交,满足题意.综上可知,
时取到“=”,经检验此时直线PQ与圆O相交,满足题意.综上可知,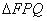 的面积的最大值为
的面积的最大值为 .(12分)
.(12分)

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 中,不等式
中,不等式 成立;在凸四边形ABCD中,不等式
成立;在凸四边形ABCD中,不等式 成立;在凸五边形ABCDE中,不等式
成立;在凸五边形ABCDE中,不等式 成立,…,依此类推,在凸n边形
成立,…,依此类推,在凸n边形 中,不等式
中,不等式 __ ___成立.
__ ___成立. ,
, ,
, .若
.若 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.

 的前
的前 项和为
项和为 ,
, ,且满足
,且满足 ,则
,则 _________.
_________.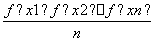 ≤f
≤f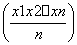 成立.已知函数y=sin x在区间上是“凸函数”,则在△ABC中,sin A+sin B+sin C的最大值是
成立.已知函数y=sin x在区间上是“凸函数”,则在△ABC中,sin A+sin B+sin C的最大值是 
 有且仅有两个极值点
有且仅有两个极值点 .
. 的取值范围;
的取值范围; ?如存在,求
?如存在,求 的极大值;如不存在,请说明理由.
的极大值;如不存在,请说明理由.