题目内容
如图:内接于⊙O的△ABC的两条高线AD、BE相交于点H,过圆心O作OF⊥BC于 F,连接AF交OH于点G,并延长CO交圆于点I.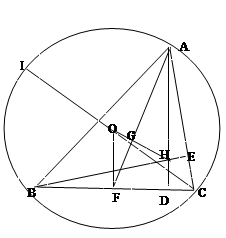
(1) 若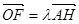 ,试求
,试求 的值;
的值;
(2)若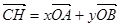 ,试求
,试求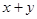 的值;
的值;
(3)若O为原点,点B的坐标为(-4,-3),点C的坐标为C(4,-3),试求点G的轨迹方程.
(1)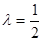 ;(2)
;(2)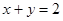 ;(3)
;(3)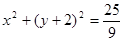 (
(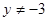 ).
).
解析试题分析:(1)利用向量共线,得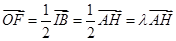 ∴
∴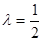 ;
;
(2)利用共面向量基本定理以及向量的加减运算,得出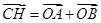 ,而
,而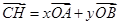
∴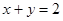 ;
;
(3)经过计算,∵OF= IB=
IB=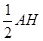 ,∴FG=
,∴FG=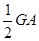 又F为BC的中点,可得出G为△ABC的重心,然后用替换的思想,设A(
又F为BC的中点,可得出G为△ABC的重心,然后用替换的思想,设A(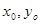 ),G(
),G( ),则
),则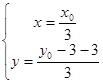 ,得:
,得: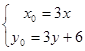 ,把动点代入已知方程,便可求出未知动点的轨迹,注意范围.
,把动点代入已知方程,便可求出未知动点的轨迹,注意范围.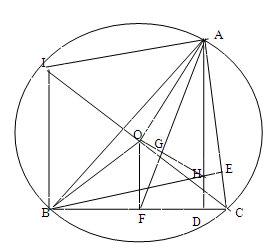
试题解析:∵CI为直径 ∴∠IAC和∠IBC均为直角
∴AI∥BE,BI∥AD∴四边形AIBH为平行四边形
(1)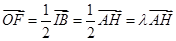 ∴
∴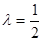
(2)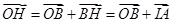
而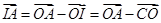
∴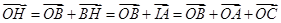
∴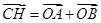 而
而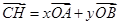
∴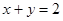
(3)∵OF= IB=
IB=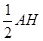 ,∴FG=
,∴FG=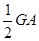 又F为BC的中点,∴G为△ABC的重心
又F为BC的中点,∴G为△ABC的重心
显然,A的轨迹为除B,C外的⊙O,其方程为: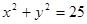 (
(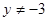 )
)
设A(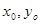 ),G(
),G( ),则
),则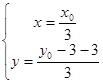 ,得:
,得: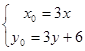 代入⊙O的方程并化简得G的轨迹方程为:
代入⊙O的方程并化简得G的轨迹方程为: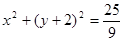 (
(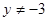 ).
).
考点:向量共线基本定理,共面向量基本定理,替换法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是平面上一点,
是平面上一点, 是平面上不共线三点,动点
是平面上不共线三点,动点 满足:
满足: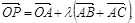
 ,已知
,已知 时,
时, .则
.则 的最小值____________.
的最小值____________.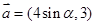 ,
,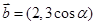 ,且
,且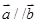 ,则锐角
,则锐角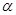 为________.
为________.


 中,
中, 分别是
分别是 的中点,
的中点, 为交点,若
为交点,若 =
= ,
, =
= ,
, 、
、 、
、 .
.
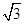 cosx-sinx),n=(sin(x+
cosx-sinx),n=(sin(x+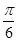 ),sinx),且满足f(x)=m·n.
),sinx),且满足f(x)=m·n. ·
· =
=

 ,且
,且 ,求
,求 .
. 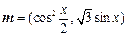 ,
,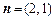 ,函数
,函数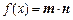 .
.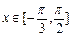 时,求函数
时,求函数 的取值范围;
的取值范围;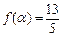 ,且
,且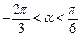 时,求
时,求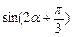 的值.
的值. -
- )·(
)·( )=0,则△ABC为________三角形.
)=0,则△ABC为________三角形. AC,在AB上取点M,使得AM=
AC,在AB上取点M,使得AM= BN,在CM的延长线上取一点Q,使MQ=λCM时,
BN,在CM的延长线上取一点Q,使MQ=λCM时, =
=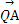 ,试确定λ的值.
,试确定λ的值.