题目内容
2.某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )
| A. | f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$ | B. | f(x)=$\frac{cosx}{x}$(-$\frac{π}{2}$$<x<\frac{π}{2}$) | ||
| C. | f(x)=$\frac{|x|}{x}$ | D. | f(x)=x2ln(x2+1) |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是输出满足条件①f(x)+f(-x)=0,即函数f(x)为奇函数②f(x)存在零点,即函数图象与x轴有交点.逐一分析四个答案中给出的函数的性质,不难得到正确答案.
解答 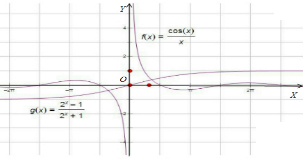 解:∵A,f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,既是奇函数,而且函数图象与x也有交点,①符合题意;
解:∵A,f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,既是奇函数,而且函数图象与x也有交点,①符合题意;
而B:f(x)=$\frac{cosx}{x}$(-$\frac{π}{2}$$<x<\frac{π}{2}$,x≠0)是奇函数,但函数图象与x无有交点,故不满足条件②;
而C:f(x)=$\frac{|x|}{x}$的函数图象与x轴没有交点,故不满足条件②;
而D:f(x)=x2ln(x2+1)明显不是奇函数,故不满足条件①;
故选:A.
点评 根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是:①分析流程图(或伪代码),从流程图(或伪代码)中即要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
12.设m=3${∫}_{-1}^{1}$(x2+sinx)}dx,则多项式(x+$\frac{1}{{m\sqrt{x}}}$)6的常数项为( )
| A. | $-\frac{5}{4}$ | B. | $\frac{5}{4}$ | C. | $-\frac{15}{16}$ | D. | $\frac{15}{16}$ |
10.如图所示的程序框图,运行相应的程序,若输出的结果是4,则常数a的值为( )


| A. | 4 | B. | 2 | C. | $\frac{1}{2}$ | D. | -1 |
7.已知椭圆mx2+4y2=1的离心率为$\frac{{\sqrt{2}}}{2}$,则实数m等于( )
| A. | 2 | B. | 2或$\frac{8}{3}$ | C. | 2或6 | D. | 2或8 |
14.设实数m,n满足m>0,n<0,且$\frac{1}{m}+\frac{1}{n}=1$,则4m+n( )
| A. | 有最小值9 | B. | 有最大值9 | C. | 有最大值1 | D. | 有最小值1 |