题目内容
△
外接圆的半径为
，圆心为
，且
， 
，则
等于
A． | B． | C． | D． |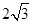
C
解析试题分析：利用向量的运算法则将已知等式化简得到
，得到BC为直径，故△ABC为直角三角形，求出三边长可得∠ACB 的值，利用两个向量的数量积的定义求出的值.因为，则可知，∴O，B，C共线，BC为圆的直径，如图
∴AB⊥AC，=1，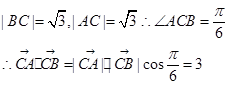
G故选C.
考点：向量的几何运用
点评：本题主要考查向量在几何中的应用、向量的数量积，向量垂直的充要条件等基本知识．求出△ABC为直角三角形及三边长，是解题的关键.
练习册系列答案
相关题目
若
(
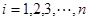)是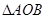
所在的平面内的点，且
.
给出下列说法：
①
；
②
的最小值一定是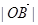
；
③点
、在一条直线上；
④向量
及
在向量
的方向上的投影必相等.
其中正确的个数是（ ）
A． 个. | B． 个. | C． 个. | D． 个. |
在△ABC中，若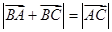
，则△ABC的形状为（ ）
| A．等腰三角形 | B．直角三角形 | C．等腰直角三角形 | D．不能确定 |
中
，点
的斜坐标定义为：“若
（其中
分别为与斜坐标系的
轴，
轴同方向的单位向量），则点
”．若
且动点
满足
，则点
在斜坐标系中的轨迹方程为（ ）
空间直角坐标系中，O为坐标原点，已知两点坐标为A（3，1，0），B（－1，3，0），若点C满足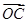
＝
＋
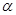
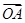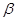
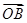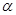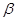，其中，∈R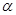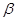，＋＝1，则点C的轨迹为
| A．平面 | B．直线 | C．圆 | D．线段 |
已知向量
，
，若
与
垂直，则
的值为 （ ）
A． | B． | C． | D． |
已知点
是
的重心，
若
，
，则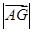
的最小值是（ ）
A． | B． | C． | D． |
已知非零向量
与
满足（
+
）·
=0,且·=-
,则△ABC为（ ）
| A．等腰非等边三角形 | B．等边三角形 |
| C．三边均不相等的三角形 | D．直角三角形 |
)．O为坐标原点，点C在第一象限，且∠AOC＝120°，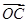
＝－3
＋λ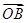
(λ∈ R)，则λ＝ .