题目内容
3.A,B两位同学各有五张卡,现以投掷均匀硬币的方式进行游戏,当出现正面朝上时A赢得B一张卡片,否则B赢得A一张卡片,如果某人已赢得所有卡片,则游戏终止;(1)求掷硬币的次数不大于7次时游戏终止的概率.
(2)设ξ表示“游戏已进行五次时同学A拥有的卡片数”,求Eξ.
分析 (1)设ξ表示游戏终止时掷硬币的次数,正面出现的次数为m,反面出现的次数为n,则$\left\{\begin{array}{l}{|m-n|=5}\\{m+n=ξ}\\{1≤ξ≤7}\end{array}\right.$.对m分类讨论即可得出.
(2)假设A赢了B,5次终止,那么A赢了4次,B赢了1次. B的这一次只能发生在前三次中(前三中还不发生,A就赢了),也就是有三种情况,每种情况概率均为$(\frac{1}{2})^{5}$,且还有B赢A的情况,则最后概率为$(\frac{1}{2})^{5}×3×2$=$\frac{3}{16}$.
解答 解:(1)设ξ表示游戏终止时掷硬币的次数,
正面出现的次数为m,反面出现的次数为n,则$\left\{\begin{array}{l}{|m-n|=5}\\{m+n=ξ}\\{1≤ξ≤7}\end{array}\right.$.
可得:当m=5,n=0或m=0,n=5时,ξ=5;
当m=6,n=1或m=1,n=6时,ξ=7.
所以ξ的所有可能取值为:5,7.
P(ξ≤7)=P(ξ=5)+P(ξ=7)=2$(\frac{1}{2})^{5}$+2${∁}_{5}^{1}×(\frac{1}{2})^{7}$=$\frac{9}{64}$.
(2)ξ表示“游戏已进行五次时同学A拥有的卡片数”,则ξ=0,1,2,3,4,7,8,9,10.
假设A赢了B,5次终止,那么A赢了4次,B赢了1次. B的这一次只能发生在前三次中(前三中还不发生,A就赢了),也就是有三种情况,每种情况概率均为$(\frac{1}{2})^{5}$,且还有B赢A的情况,则最后概率为$(\frac{1}{2})^{5}×3×2$=$\frac{3}{16}$.
点评 本题考查了二项分布列的概率与首项期望计算公式、古典概率计算公式,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{10}}{5}$ |
| A. | {0,2} | B. | {0,1,2} | C. | {1,2} | D. | {0,1} |
| A. | {-2,-1} | B. | {0,1} | C. | {-1,0,1} | D. | {0,1,2} |
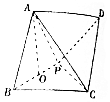 如图,在四棱锥P-ABCD中,底面ABCD是菱形,且AB=$\sqrt{2}$,∠ABC=60°,点A在平面PBC上的射影为PB的中点O,PB⊥AC.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,且AB=$\sqrt{2}$,∠ABC=60°,点A在平面PBC上的射影为PB的中点O,PB⊥AC.