Question

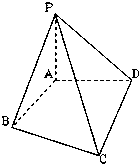如图，已知PA⊥面ABCD，PA=AB=AD=

1

2

CD，∠BAD=∠ADC=90°
（1）在面PCD上找一点M，使BM⊥面PCD；
（2）求由面PBC与面PAD所成角的二面角的余弦值．

Answer 1

分析：（1）设M为PC的中点，PD中点为N，由条件可得ABMN为平行四边形，BM∥AN．再根据AN⊥面PCD，可得BM⊥面PCD．
（2）延长CB交DA于E，证明PE⊥面PCD，可得∠CPD为二面角C-PE-D的平面角．求得得tan∠CPD=

2

，可得cos∠CPD的值．

解答：解：（1）M为PC的中点，设PD中点为N，则MN=

1

2

CD，且MN∥

1

2

CD，∴MN=AB，MN∥AB．
再由 PA=AB=AD=

1

2

CD，可得ABMN为平行四边形，∴BM∥AN．
可得∠PAD=90°，∴AN⊥PD，又CD⊥AN，∴AN⊥面PCD，∴BM⊥面PCD．…（6分）
（2）延长CB交DA于E，∵AB=

1

2

CD，且AB∥

1

2

CD，∴AE=AD=PA，∴PD⊥PE．
又∴PE⊥CD，∴PE⊥面PCD，∴∠CPD为二面角C-PE-D的平面角．
再由PD=

2

AD，CD=2AD，可得tan∠CPD=

2

，
∴cos∠CPD=

3

3

．…（12分）

点评：本题主要考查直线和平面平行的判定定理的应用，求二面角的平面角的方法，体现了转化的数学思想，属于中档题．