题目内容
已知函数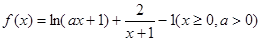 .
.
(1)若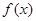 在
在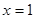 处取得极值,求
处取得极值,求 的值;
的值;
(2)求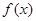 的单调区间;
的单调区间;
(3)若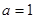 且
且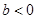 ,函数
,函数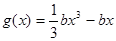 ,若对于
,若对于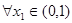 ,总存在
,总存在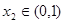 使得
使得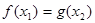 ,求实数
,求实数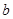 的取值范围.
的取值范围.
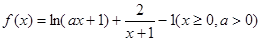 .
.(1)若
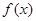 在
在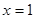 处取得极值,求
处取得极值,求 的值;
的值;(2)求
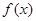 的单调区间;
的单调区间;(3)若
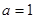 且
且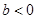 ,函数
,函数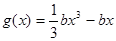 ,若对于
,若对于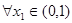 ,总存在
,总存在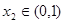 使得
使得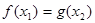 ,求实数
,求实数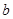 的取值范围.
的取值范围.(1) ;(2)
;(2)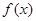 的单调减区间是
的单调减区间是 ,单调增区间是
,单调增区间是  ;(3)
;(3) .
.
 ;(2)
;(2)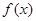 的单调减区间是
的单调减区间是 ,单调增区间是
,单调增区间是  ;(3)
;(3) .
.试题分析:(1)首先求函数
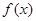 的导数,再解方程
的导数,再解方程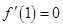 即可求得
即可求得 的值;(2)根据
的值;(2)根据 结合
结合 的取值及
的取值及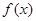 的定义域分类讨论求
的定义域分类讨论求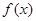 的单调区间;(3)由已知“对于
的单调区间;(3)由已知“对于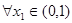 ,总存在
,总存在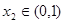 使得
使得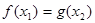 ”,知函数
”,知函数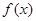 的值域是函数
的值域是函数 的值域的子集.先利用导数求函数
的值域的子集.先利用导数求函数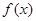 ,
, 的值域,最后利用集合的包含关系求出实数
的值域,最后利用集合的包含关系求出实数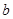 的取值范围.
的取值范围.试题解析:(1)

 1分
1分由
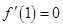 得, 2分
得, 2分 3分
3分(2)

若
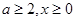 ,得
,得 4分
4分即
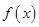 在
在 上单调递增, 5分
上单调递增, 5分若
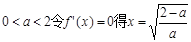 或
或 (舍去) 6分
(舍去) 6分 |  |  | 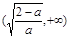 |
 | - | 0 | + |
 | 单调减 | | 单调增 |
 的单调减区间是
的单调减区间是 ,单调增区间是
,单调增区间是  , 9分
, 9分(3)
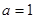 由(2)得
由(2)得 在
在 上是减函数,
上是减函数, ,即
,即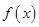 值域
值域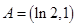 10分
10分又

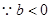
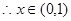 时
时

 在
在 上递增. 11分
上递增. 11分 的值域
的值域 12分
12分由
 使得
使得 ,
, 13分
13分即

 14分
14分
练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
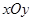 中,点
中,点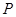 到两点
到两点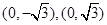 的距离之和等于4,设点
的距离之和等于4,设点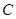 ,直线
,直线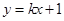 与
与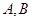 两点.
两点.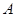 在第一象限,证明当
在第一象限,证明当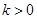 时,恒有
时,恒有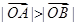 .
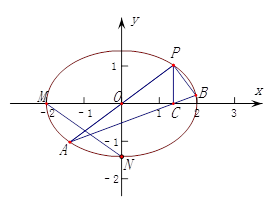
.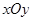 中,
中,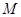 、
、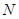 分别是椭圆
分别是椭圆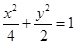 的顶点,过坐标原点的直线交椭圆于
的顶点,过坐标原点的直线交椭圆于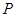 、
、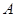 两点,其中
两点,其中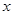 轴的垂线,垂足为
轴的垂线,垂足为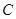 .连接
.连接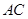 ,并延长交椭圆于点
,并延长交椭圆于点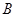 .设直线
.设直线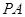 的斜率为
的斜率为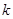 .
.
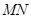 时,求
时,求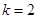 时,求点
时,求点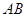 的距离;
的距离;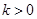 ,求证:
,求证: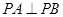 .
.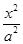 +
+ =1(a>b>0)的焦距为4,且与椭圆x2+
=1(a>b>0)的焦距为4,且与椭圆x2+ =1有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同的两点A、B.
=1有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同的两点A、B.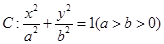 的左、右焦点分别为
的左、右焦点分别为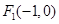 、
、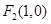 ,P为椭圆
,P为椭圆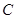 上任意一点,且
上任意一点,且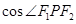 的最小值为
的最小值为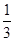 .
.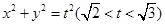 与椭圆
与椭圆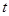 为何值时,矩形ABCD的面积取得最大值?并求出其最大面积.
为何值时,矩形ABCD的面积取得最大值?并求出其最大面积. 的焦点
的焦点 与椭圆
与椭圆 的一个焦点重合,它们在第一象限内的交点为
的一个焦点重合,它们在第一象限内的交点为 ,且
,且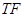 与
与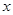 轴垂直,则椭圆的离心率为( )
轴垂直,则椭圆的离心率为( ) 



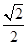
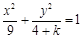 的离心率为
的离心率为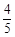 ,则k的值为( )
,则k的值为( ) 或21
或21 或21
或21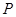 为椭圆
为椭圆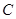 上一点,
上一点,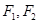 为两焦点,
为两焦点,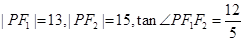 ,则椭圆
,则椭圆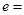 .
. 的左焦点为F
的左焦点为F





