题目内容
已知α、β都是锐角,且sinβsinα=cos(α+β).(1)求证:tanβ=![]() ;
;
(2)当tanβ取最大值时,求tan(α+β)的值.
(1)证明:由已知得?
sinβ=sinαcos(α+β)=sinαcosαcosβ-sin2αsinβ, ?
∴tanβ=sinαcosα-sin2αtanβ. ?
∴tanβ=![]() =
=![]() =
=![]() ,即tanβ=
,即tanβ=![]() . ?
. ?
(2)解:∵α是锐角,∴tanα>0.?
由(1)知tanβ=![]() ,?
,?
∴![]() =
=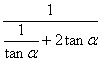 ≤
≤![]() =
=![]() ,当且仅当
,当且仅当![]() =2tanα时,等号成立,
=2tanα时,等号成立,
即tanα=![]() 时,tanβ取最大值
时,tanβ取最大值![]() . ?
. ?
此时tan(α+β)=![]() =
=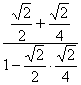 =
=![]() .
.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
 ,(1+tanA)(1+tanB)=2,求证A+B=45°.
,(1+tanA)(1+tanB)=2,求证A+B=45°.