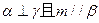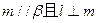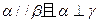题目内容
(本题满分8分)
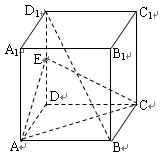
如图,在正方体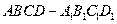 中,
中,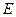 是
是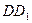 的中点,
的中点,
求证:
(1)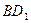 ∥平面
∥平面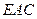 ;
;
(2)求异面直线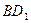 与
与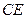 所成角的余弦值.
所成角的余弦值.
如图,在正方体
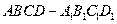 中,
中,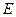 是
是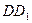 的中点,
的中点,求证:

(1)
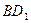 ∥平面
∥平面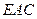 ;
;(2)求异面直线
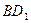 与
与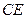 所成角的余弦值.
所成角的余弦值.(1)略(2)

(1)证明:连结 ,连接
,连接 ,则
,则 ,
,
(2)
 所成的角就是
所成的角就是 所成的角.设正方体的棱长为1,则在三角形
所成的角.设正方体的棱长为1,则在三角形 中,可求
中,可求 又
又 所以,
所以,
 即所求.
即所求.
 ,连接
,连接 ,则
,则 ,
,
(2)

 所成的角就是
所成的角就是 所成的角.设正方体的棱长为1,则在三角形
所成的角.设正方体的棱长为1,则在三角形 中,可求
中,可求 又
又 所以,
所以, 即所求.
即所求.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
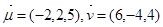 分别是平面
分别是平面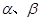 的法向量,则平面
的法向量,则平面 中,各棱长均为2,平面
中,各棱长均为2,平面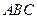 ⊥平 面
⊥平 面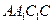 ,
,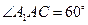 .
.
 ⊥平面
⊥平面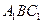 ;
;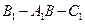 的大小;
的大小;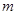 、
、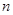 与平面
与平面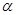 、
、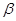 ,下列命题正确的是 ( )
,下列命题正确的是 ( )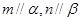 且
且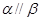 ,则
,则
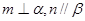 且
且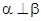 ,则
,则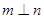
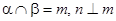 且
且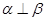 ,则
,则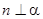
 且
且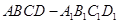 ,长为2的线段
,长为2的线段 的一个端点
的一个端点 在
在 上
上 在底面
在底面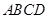 上运动.则线段
上运动.则线段 的轨迹与正方体的表面所
的轨迹与正方体的表面所



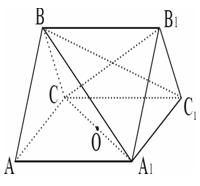
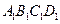 中E是AB的中点,O是侧面
中E是AB的中点,O是侧面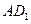 的中心.
的中心.








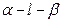 的棱
的棱 上有
上有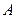 ,
,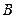 两点,直线
两点,直线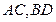 分别在这个二面角的两个半平面内,且都垂直于
分别在这个二面角的两个半平面内,且都垂直于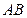 ,若
,若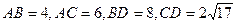 ,则二面角
,则二面角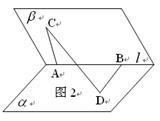
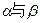 所成的二面角为80°,P为
所成的二面角为80°,P为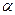 、
、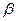 外一定点,过点P的一条直线与
外一定点,过点P的一条直线与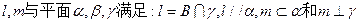 ,那么必有( )
,那么必有( )