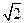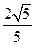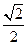题目内容
(本小题满分12分)
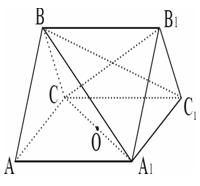
已知三棱柱 中,各棱长均为2,平面
中,各棱长均为2,平面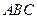 ⊥平 面
⊥平 面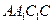 ,
,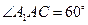 .
.
(1)求证: ⊥平面
⊥平面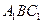 ;
;
(2)求二面角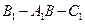 的大小;
的大小;
已知三棱柱
 中,各棱长均为2,平面
中,各棱长均为2,平面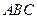 ⊥平 面
⊥平 面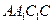 ,
,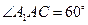 .
.
(1)求证:
 ⊥平面
⊥平面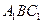 ;
;(2)求二面角
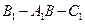 的大小;
的大小;(1)略(2)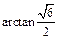
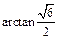
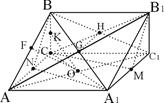
(I)证明:取A1C1的中点M,连CM、B1M
∵三棱柱ABC-A1B1C1,∴各棱长均相等,∠A1AC=60°
∴△A1CC1与△A1B1C1都是等边三角形
∴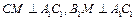
∵平面ABC⊥平面AA1C1C,
∴平面A1B1C1⊥平面AA1C1C
∴B1M⊥平面AA1C1C,由三垂线定理得:B1C⊥A1C1
又∵四边形BCC1B1是菱形,∴B1C⊥BC1
而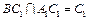
∴B1C⊥平面A1BC1
(II)法一:连AB1与A1B交于G点,设B1C与BC1交于H点,连GH,则GH
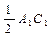

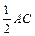
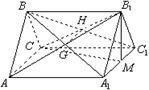
取AC的中点N,连BN,A1N,可证AC⊥A1B ∴GH⊥A1B
又∵四边形AA1B1B是菱形 ∴AB1⊥A1B
∴∠B1GH就是所求二面角的平面角;
法二:由(I)知,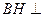 平面
平面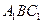 ,
,
又四边形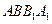 是菱形,所以
是菱形,所以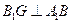 ,由三垂线定理的逆定理得,
,由三垂线定理的逆定理得,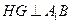 ,所以
,所以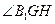 就是二面角B1-A1B-C1的平面角
就是二面角B1-A1B-C1的平面角
由(1)知A1C1⊥B1C ∴GH⊥B1C
设A1C1=a,则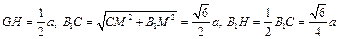
∴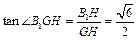 即所求二面角的大小为
即所求二面角的大小为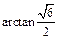
∵三棱柱ABC-A1B1C1,∴各棱长均相等,∠A1AC=60°
∴△A1CC1与△A1B1C1都是等边三角形
∴
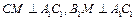
∵平面ABC⊥平面AA1C1C,
∴平面A1B1C1⊥平面AA1C1C
∴B1M⊥平面AA1C1C,由三垂线定理得:B1C⊥A1C1
又∵四边形BCC1B1是菱形,∴B1C⊥BC1
而
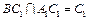

∴B1C⊥平面A1BC1
(II)法一:连AB1与A1B交于G点,设B1C与BC1交于H点,连GH,则GH

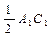

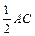

取AC的中点N,连BN,A1N,可证AC⊥A1B ∴GH⊥A1B
又∵四边形AA1B1B是菱形 ∴AB1⊥A1B
∴∠B1GH就是所求二面角的平面角;
法二:由(I)知,
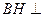 平面
平面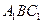 ,
,又四边形
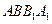 是菱形,所以
是菱形,所以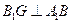 ,由三垂线定理的逆定理得,
,由三垂线定理的逆定理得,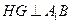 ,所以
,所以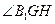 就是二面角B1-A1B-C1的平面角
就是二面角B1-A1B-C1的平面角由(1)知A1C1⊥B1C ∴GH⊥B1C
设A1C1=a,则
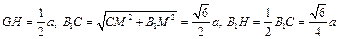
∴
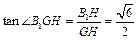 即所求二面角的大小为
即所求二面角的大小为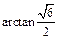

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
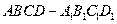 中,
中,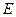 是
是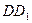 的中点,
的中点,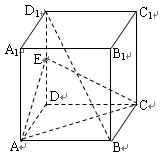
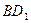 ∥平面
∥平面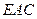 ;
;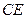 所成角的余弦值.
所成角的余弦值.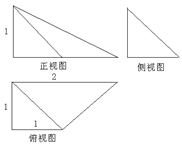
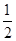
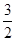

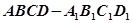 中,过顶点
中,过顶点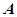 任作一条直线
任作一条直线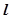 ,与异面直线
,与异面直线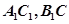
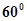 ,则这样的直线
,则这样的直线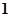 条
条 条
条 条
条 条
条 点,那么求异面直线EF与SA所成的角。
点,那么求异面直线EF与SA所成的角。 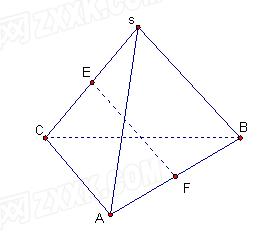
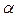 、
、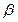 ,则下列命题中错误的是 ( )
,则下列命题中错误的是 ( )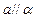 ,且
,且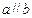 ,则
,则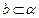 或
或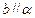
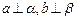 ,则
,则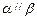
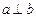 ,且
,且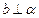
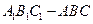 中,
中, ,
, ,点G与E分别为线段
,点G与E分别为线段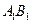 和
和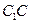 的中点,点D与F分别为线段AC和AB上的动点。若
的中点,点D与F分别为线段AC和AB上的动点。若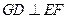 ,则线段DF长度的最小值是( )
,则线段DF长度的最小值是( )