Question

【题目】已知集合.

（1）若，且为整数，求的概率；

（2）若，求的概率.

Answer 1

【答案】（1）（2）

【解析】

（1）因为x，y∈Z，且x∈[0，2]，y∈[﹣1，1]，基本事件是有限的，所以为古典概型，这样求得总的基本事件的个数，再求得满足x，y∈Z，x+y≥0的基本事件的个数，然后求比值即为所求的概率；

（2）因为，几何概型中的面积类型，先求∈表示的区域的面积，再求x+y≥0表示的区域的面积，然后求比值即为所求的概率.

解：（1）设“，”为事件，，，

即；，即.

则基本事件有：，，，，，，，，共9个，其中满足的基本事件有8个，

所以.

故，的概率为.

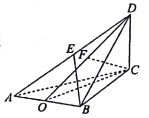
（2）设“，”为事件，因为，，则基本事件为如图四边形区域，事件包括的区域为其中的阴影部分.

所以 ，

故“，”的概率为.