题目内容
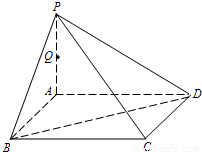
如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.
(1)求证:PC⊥BD;
(2)求点Q到BD的距离.
(1)求证:PC⊥BD;
(2)求点Q到BD的距离.


(1)连接AC
∵PA⊥AB,PA⊥AD,AB∩AD=A
∴PA⊥平面ABCD
∴AC为斜线PC在平面ABCD内的射影
∵ABCD是正方形
∴AC⊥BD(4分)
∴PC⊥BD(6分)
(2)设AC∩BD=O,连接OQ
∵Q为PA中点,O为AC中点
∴OQ∥PC
∵PC⊥BD
∴OQ⊥BD
∴OQ的长就是点Q到BD的距离(9分)
∵AB=2,PA=4
∴AC=2
| 2 |
∴OA=
| 2 |
∴OQ=
| QA2+OA2 |
| 6 |
即点Q到BD的距离为
| 6 |

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
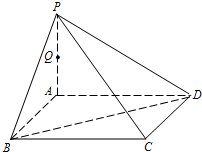 如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.
如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.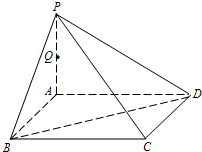 如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.
如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.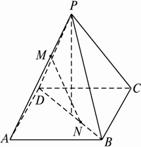
 如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.
如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.