Question

A={（x，y）|-2≤x≤2，-2≤y≤2}，b={（x，y）|x²+y²≥1}．若在区域A中随机的扔一颗豆子，求该豆子落在区域B中的概率为（　　）

• A．

  π

  16

• B．1-

  π

  16

• C．

  π

  4

• D．1-

  π

  4

Answer 1

分析：先求出区域A的面积，然后利用圆的面积公式求区域B的面积，最后利用几何概型的概率公式解之即可．

解答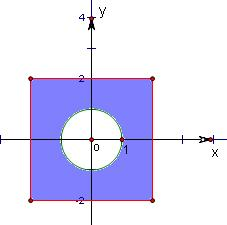：解：集合M={（x，y）|-2≤x≤2，-2≤y≤2}表示的区域是一正方形，其面积为16，
集合B={（x，y）丨x²+y²≥1}表示的区域为图中阴影部分，其面积为16-π．
∴向区域A内随机抛掷一粒豆子，则豆子落在区域B内的概率为 

16-π

16

=1-

π

16

．
故选B．

点评：本题主要考查了几何概型的概率，以及利用圆的面积公式求区域面积，属于中档题．