题目内容
已知函数f(x)是定义域为R的奇函数,当x>0时,
f(x)=x2-2x.
(1)求出函数f(x)在R上的解析式;
(2)画出函数f(x)的图象.
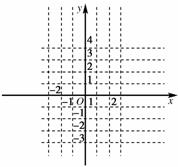
解析: (1)①由于函数f(x)是定义域为R的奇函数,
则f(0)=0;
②当x<0时,-x>0,∵f(x)是奇函数,
∴f(-x)=-f(x),
∴f(x)=-f(-x)
=-[(-x)2-2(-x)]
=-x2-2x,
综上:f(x)=
(2)图象如图:


练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
 的定义域
的定义域 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 ,则f(-1)=( )
,则f(-1)=( )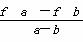 >0成立,则必有( )
>0成立,则必有( )
 为定义在
为定义在 上的奇函数,当
上的奇函数,当 时,函数解析式为
时,函数解析式为 .
. 上的解析式; (Ⅱ)求
上的解析式; (Ⅱ)求