题目内容
设函数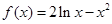 .
.
(I)求函数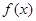 的单调递增区间;
的单调递增区间;
(II) 若关于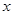 的方程
的方程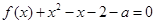 在区间
在区间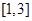 内恰有两个不同的实根,求实数
内恰有两个不同的实根,求实数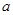 的取值范围.
的取值范围.
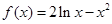 .
.(I)求函数
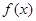 的单调递增区间;
的单调递增区间;(II) 若关于
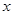 的方程
的方程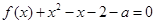 在区间
在区间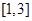 内恰有两个不同的实根,求实数
内恰有两个不同的实根,求实数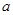 的取值范围.
的取值范围.(Ⅰ) ;(Ⅱ)
;(Ⅱ)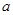 的取值范围是
的取值范围是
 ;(Ⅱ)
;(Ⅱ)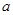 的取值范围是
的取值范围是
试题分析:(Ⅰ)求出导数,根据导数大于0求得
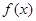 的单调递增区间.
的单调递增区间.(Ⅱ)令
 .利用导数求出
.利用导数求出 的单调区间和极值点,画出其简图,结合函数零点的判定定理找出
的单调区间和极值点,画出其简图,结合函数零点的判定定理找出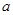 所满足的条件,由此便可求出
所满足的条件,由此便可求出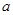 的取值范围.
的取值范围.试题解析:(Ⅰ)函数
 的定义域为
的定义域为 ,
, ∵
 ,
, ∵
 ,则使
,则使 的
的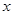 的取值范围为
的取值范围为 ,
, 故函数
 的单调递增区间为
的单调递增区间为
(Ⅱ)∵
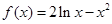 ,
, ∴

令
 ,
, ∵
 ,且
,且 ,
, 由
 得
得 ,由
,由 得
得 .
. ∴
 在区间
在区间 内单调递减,在区间
内单调递减,在区间 内单调递增,
内单调递增, 故
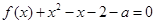 在区间
在区间 内恰有两个相异实根
内恰有两个相异实根 
即
 解得:
解得: .
. 综上所述,
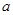 的取值范围是
的取值范围是

练习册系列答案
相关题目
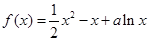 (其中
(其中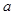 为常数).
为常数).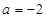 时,求函数
时,求函数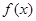 的最值;
的最值;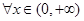 都有
都有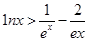 。
。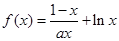 .
.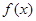 在
在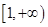 上是增函数,求正实数
上是增函数,求正实数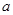 的取值范围;
的取值范围;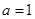 ,
,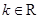 且
且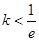 ,设
,设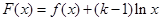 ,求函数
,求函数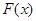 在
在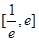 上的最大值和最小值.
上的最大值和最小值.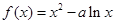 和
和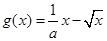 ,且
,且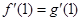 .
.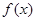 ,
,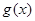 的表达式;
的表达式;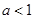 时,不等式
时,不等式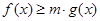 在
在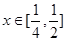 上恒成立,求实数
上恒成立,求实数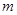 的取值范围.
的取值范围.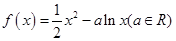 .
.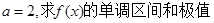 .
.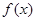 在
在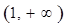 上是增函数,求
上是增函数,求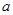 的取值范围.
的取值范围.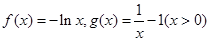 .
.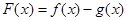 的极值,并证明:若
的极值,并证明:若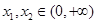 有
有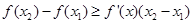 ;
; 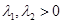 ,且
,且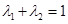 ,
,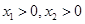 ,证明:
,证明: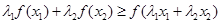 ,
,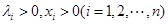 ,由上述结论猜想一个一般性结论(不需要证明);
,由上述结论猜想一个一般性结论(不需要证明);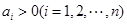 ,则
,则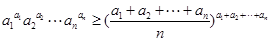 .
.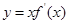 的图象如图所示(其中
的图象如图所示(其中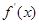 是函数
是函数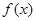 的导函数)下面四个图象中,
的导函数)下面四个图象中,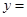
 ,则函数
,则函数 的单调递增区间是________.
的单调递增区间是________.