题目内容
【题目】设抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 的面积为
的面积为![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() ,
,![]() 是
是![]() 上的两个动点,
上的两个动点,![]() ,试问:是否存在定点
,试问:是否存在定点![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】(1)![]() ;
;
(2)见解析.
【解析】
(1)把![]() 代入抛物线方程可得:
代入抛物线方程可得:![]() ,解得
,解得![]() .根据
.根据![]() 的面积为
的面积为![]() 列方程,解得
列方程,解得![]() ,问题得解.
,问题得解.
(2)假设存在定点S,使得![]() .设
.设![]() ,线段
,线段![]() 的中点为
的中点为![]() .由
.由![]() ,可得
,可得![]() ,化为:
,化为:![]() .当
.当![]() 轴时满足题意,因此点S必然在x轴上.设直线
轴时满足题意,因此点S必然在x轴上.设直线![]() 的方程为:
的方程为:![]() .与抛物线方程联立可得:
.与抛物线方程联立可得:![]() .根据根与系数的关系、中点坐标公式可得
.根据根与系数的关系、中点坐标公式可得![]() .可得线段
.可得线段![]() 的垂直平分线方程,问题得解.
的垂直平分线方程,问题得解.
解:(1)把![]() 代入抛物线方程
代入抛物线方程![]() ,可得:
,可得:![]() ,解得
,解得![]() .
.
∵![]() 的面积为
的面积为![]() .
.
∴![]() ,解得
,解得![]() .
.
∴E的方程为:![]() .
.
(2)假设存在定点S,使得![]() .
.
设![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
由抛物线定义可得:![]() ,
,![]()
∵![]() ,
,
∴![]() ,整理得:
,整理得:![]() .∴
.∴![]() .
.
当![]() 轴时满足题意,因此点S必然在x轴上.
轴时满足题意,因此点S必然在x轴上.
设直线![]() 的方程为:
的方程为:![]() .
.
联立![]() ,化为:
,化为:![]() .
.
∴![]() ,
,
∴![]() .
.
线段![]() 的垂直平分线方程为:
的垂直平分线方程为:![]() ,
,
令![]() ,可得:
,可得:![]() .
.
∴存在定点![]() ,使得
,使得![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】![]() 是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物),为了探究车流量与
是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物),为了探究车流量与![]() 的浓度是否相关,现采集到某城市周一至周五某时间段车流量与
的浓度是否相关,现采集到某城市周一至周五某时间段车流量与![]() 浓度的数据如下表:
浓度的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 39 | 40 | 42 | 44 | 45 |
(1)根据上表数据,求出这五组数据组成的散点图的样本中心坐标;
(2)用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若周六同一时间段车流量是100万辆,试根据(2)求出的线性回归方程预测,此时![]() 的浓度是多少?
的浓度是多少?
(参考公式: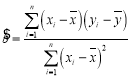 ,
,![]() )
)