题目内容
已知 等于
等于
- A.

- B.

- C.-

- D.

D
分析:由题意可得- =
= +
+ ,平方化简可得
,平方化简可得  ,故以
,故以 、
、 为邻边的平行四边形是一个菱形,从而得到
为邻边的平行四边形是一个菱形,从而得到 、
、 的夹角等于150°,从而求得cos<
的夹角等于150°,从而求得cos< ,
, >的值.
>的值.
解答: 解:由题意可得-
解:由题意可得- =
= +
+ ,平方可得 3
,平方可得 3 =
= =
= .
.
即2 =
= •|
•| |+
|+ ,
, -
- =
= •|
•| |-
|- ,
,
∴( )(
)( )=
)= (
( ),
),
化简可得 ( )•(2
)•(2 +
+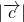 )=0,∴
)=0,∴ .
.
故以 、
、 为邻边的平行四边形是一个菱形.
为邻边的平行四边形是一个菱形.
如图所示:设 =
= ,
, =
= ,则
,则 =
= ,s设
,s设  =-
=- ,
,
由 与
与 的夹角等于60°,可得∠BAD=60°,∠BAC=30°,故∠MAB=150°,即
的夹角等于60°,可得∠BAD=60°,∠BAC=30°,故∠MAB=150°,即 、
、 的夹角等于150°,
的夹角等于150°,
∴cos< ,
, >=cos150°=-
>=cos150°=- ,
,
故选D.
点评:本题主要考查两个向量的数量积的定义,判断以 、
、 为邻边的平行四边形是一个菱形,是解题的关键,体现了数形结合的数学思想,属于中档题.
为邻边的平行四边形是一个菱形,是解题的关键,体现了数形结合的数学思想,属于中档题.
分析:由题意可得-
 =
= +
+ ,平方化简可得
,平方化简可得  ,故以
,故以 、
、 为邻边的平行四边形是一个菱形,从而得到
为邻边的平行四边形是一个菱形,从而得到 、
、 的夹角等于150°,从而求得cos<
的夹角等于150°,从而求得cos< ,
, >的值.
>的值.解答:
 解:由题意可得-
解:由题意可得- =
= +
+ ,平方可得 3
,平方可得 3 =
= =
= .
.即2
 =
= •|
•| |+
|+ ,
, -
- =
= •|
•| |-
|- ,
,∴(
 )(
)( )=
)= (
( ),
),化简可得 (
 )•(2
)•(2 +
+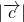 )=0,∴
)=0,∴ .
.故以
 、
、 为邻边的平行四边形是一个菱形.
为邻边的平行四边形是一个菱形.如图所示:设
 =
= ,
, =
= ,则
,则 =
= ,s设
,s设  =-
=- ,
,由
 与
与 的夹角等于60°,可得∠BAD=60°,∠BAC=30°,故∠MAB=150°,即
的夹角等于60°,可得∠BAD=60°,∠BAC=30°,故∠MAB=150°,即 、
、 的夹角等于150°,
的夹角等于150°,∴cos<
 ,
, >=cos150°=-
>=cos150°=- ,
,故选D.
点评:本题主要考查两个向量的数量积的定义,判断以
 、
、 为邻边的平行四边形是一个菱形,是解题的关键,体现了数形结合的数学思想,属于中档题.
为邻边的平行四边形是一个菱形,是解题的关键,体现了数形结合的数学思想,属于中档题. 
练习册系列答案
相关题目
 ,当x=b时取到极大值c,则ad等于( )
,当x=b时取到极大值c,则ad等于( ) B.0
C.1
D.2
B.0
C.1
D.2 如图,已知
如图,已知 等于
等于



 等于
等于


