题目内容
【题目】定义:如果函数f(x)在[a,b]上存在x1 , x2(a<x1<x2<b)满足 ![]() ,
, ![]() 则称函数f(x)是[a,b]上的“中值函数”.已知函数
则称函数f(x)是[a,b]上的“中值函数”.已知函数 ![]() 是[0,m]上的“中值函数”,则实数m的取值范围是( )
是[0,m]上的“中值函数”,则实数m的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:由题意可知, 在区间[0,m]存在x1 , x2(0<x1<x2<a),
满足f′(x2)= ![]() =
= ![]() ,
,
∵ ![]() ,
,
∴f′(x)=x2﹣x,
∴方程x2﹣x= ![]() 在区间(0,m)有两个解.
在区间(0,m)有两个解.
令g(x)=x2﹣x﹣ ![]() ,(0<x<m)
,(0<x<m)
则 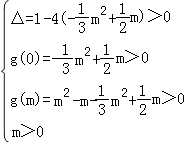
解得 ![]() <m<
<m< ![]() ,
,
∴实数m的取值范围是( ![]() ,
, ![]() ).
).
故选:B
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.

练习册系列答案
相关题目