题目内容
某地拟模仿图甲建造一座大型体育馆,其设计方案侧面的外轮廓线如图乙所示:曲线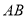 是以点
是以点 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中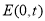 (
( ,单位:米);曲线
,单位:米);曲线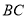 是抛物线
是抛物线 的一部分;
的一部分;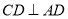 ,且
,且 恰好等于圆
恰好等于圆 的半径. 假定拟建体育馆的高
的半径. 假定拟建体育馆的高 米.
米.

(1)若要求 米,
米,
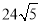 米,求
米,求 与
与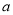 的值;
的值;
(2)若要求体育馆侧面的最大宽度 不超过
不超过 米,求
米,求 的取值范围;
的取值范围;
(3)若 ,求
,求 的最大值.
的最大值.
(参考公式:若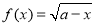 ,则
,则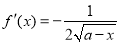 )
)
(1)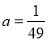 ,(2)
,(2)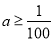 ,(3)25
,(3)25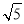 .
.
【解析】
试题分析:(1)曲线为圆与抛物线的结合体,由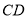 恰好等于圆
恰好等于圆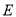 的半径得
的半径得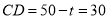 ,
,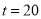 ,从而可得圆的方程
,从而可得圆的方程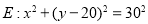 ,令
,令 ,得
,得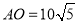 ,再根据
,再根据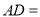
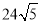 得点
得点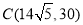 进而解出
进而解出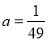 .(2)
.(2)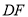 为圆半径与OD之和,圆
为圆半径与OD之和,圆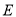 的半径为
的半径为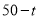 ,关键求OD:因为
,关键求OD:因为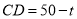 ,所以在
,所以在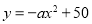 中令
中令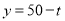 ,得
,得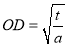 ,问题就转化为
,问题就转化为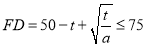 对
对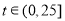 恒成立,利用变量分离法可得
恒成立,利用变量分离法可得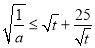 恒成立,因为
恒成立,因为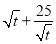 最小值10,所以
最小值10,所以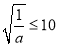 ,解得
,解得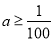 . (3)当
. (3)当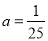 时,
时,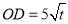 ,由圆的方程可得
,由圆的方程可得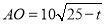 ,从而
,从而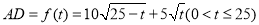 ,这要利用导数求其最值.
,这要利用导数求其最值.
试题解析:(1)因为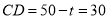 ,解得
,解得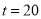 . 2分
. 2分
此时圆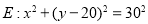 ,令
,令 ,得
,得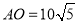 ,
,
所以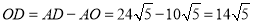 ,将点
,将点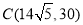 代入
代入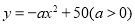 中,
中,
解得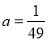 . 4分
. 4分
(2)因为圆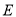 的半径为
的半径为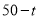 ,所以
,所以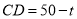 ,在
,在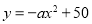 中令
中令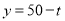 ,得
,得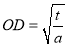 ,
,
则由题意知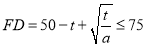 对
对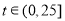 恒成立, 8分
恒成立, 8分
所以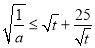 恒成立,而当
恒成立,而当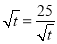 ,即
,即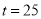 时,
时,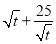 取最小值10,
取最小值10,
故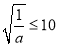 ,解得
,解得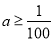 . 10分
. 10分
(3)当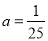 时,
时,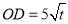 ,又圆
,又圆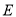 的方程为
的方程为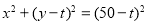 ,令
,令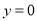 ,得
,得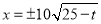 ,所以
,所以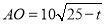 ,
,
从而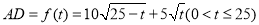 , 12分
, 12分
又因为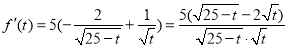 ,令
,令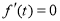 ,得
,得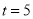 , 14分
, 14分
当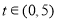 时,
时,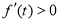 ,
,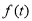 单调递增;当
单调递增;当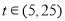 时,
时,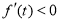 ,
,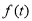 单调递减,从而当
单调递减,从而当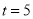 时,
时,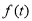 取最大值为25
取最大值为25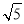 .
.
答:当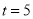 米时,
米时,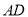 的最大值为25
的最大值为25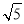 米. 16分
米. 16分
考点:函数解析式,不等式恒成立,利用导数求最值

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 的底面边长为1,异面直线
的底面边长为1,异面直线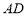 与
与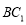 所成角的大小为
所成角的大小为 ,求:
,求:
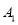
 到底面
到底面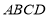 的距离;
的距离;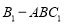 的体积。
的体积。 ,则
,则 =________________.
=________________.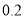 ,甲、乙下和棋的概率为
,甲、乙下和棋的概率为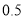 ,则乙获胜的概率为 .
,则乙获胜的概率为 . 的圆心到直线
的圆心到直线 的距离.
的距离. 是定义在
是定义在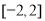 上的奇函数,当
上的奇函数,当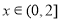 时,
时, ,函数
,函数 . 如果对于
. 如果对于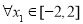 ,
,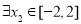 ,使得
,使得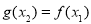 ,则实数
,则实数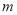 的取值范围是 .
的取值范围是 .
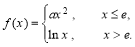 ,其中
,其中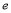 是自然对数的底数,若直线
是自然对数的底数,若直线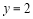 与函数
与函数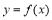 的图象有三个交点,则常数
的图象有三个交点,则常数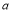 的取值范围是
的取值范围是 B.
B.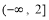 C.
C.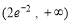 D.
D.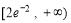
 (
( 为参数)上,则|AB|的最大值为 .
为参数)上,则|AB|的最大值为 .