题目内容
已知向量 向量
向量 记
记
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若 ,求函数
,求函数 的值域.
的值域.
(1) (2)
(2)
解析试题分析:(1)根据向量的数量积利用三角恒等变换将 化为
化为 求单调区间只需满足不等式
求单调区间只需满足不等式 即可,解这个不等式得到
即可,解这个不等式得到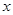 的区间即为增区间;
的区间即为增区间;
(2)求 在区间
在区间 上的值域时要先求
上的值域时要先求 得这个整体的范围
得这个整体的范围 ,再求
,再求 在
在 上的值域.容易犯的错误就是直接把区间
上的值域.容易犯的错误就是直接把区间 的两个端点
的两个端点 给代入
给代入 求得两个端点值当作值域,求值域必需分析在整个区间上的单调性变化规律,不能只求两个端点值.
求得两个端点值当作值域,求值域必需分析在整个区间上的单调性变化规律,不能只求两个端点值.
试题解析:(1)
由 得
得
故函数 的单调递增区间为
的单调递增区间为
(2)由 ,得
,得 ,
,
所以
所在 的值域为
的值域为
考点:1、三角恒等变换;2、三角函数在区间上的值域.

练习册系列答案
相关题目
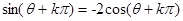
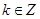
 ;
; 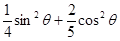
 中,内角A,B,C所对的边分别为a,b,c,且
中,内角A,B,C所对的边分别为a,b,c,且 .
. ,
, 为
为 的最大值,并指出此时B的值.
的最大值,并指出此时B的值. 的最小正周期和最小值;并写出该函数在
的最小正周期和最小值;并写出该函数在 上的单调递增区间.
上的单调递增区间.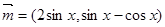 ,
, ,函数
,函数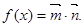
 的解析式;
的解析式; 中,角
中,角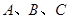 的对边为
的对边为 ,若
,若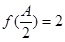 ,
,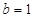 ,
,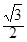 ,求a的值.
,求a的值.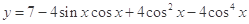 的最大值与最小值.
的最大值与最小值. ,求下列各式的值:
,求下列各式的值: ;
; .
. (
( ),其图象相邻两条对称轴之间的距离等于
),其图象相邻两条对称轴之间的距离等于 .
. 的值;
的值; 时,求函数
时,求函数 的最大值和最小值及相应的
的最大值和最小值及相应的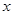 值.
值. ,点P,Q分别是在角A的两边上不同于点A的动点.
,点P,Q分别是在角A的两边上不同于点A的动点.
 ,求AQ的长;
,求AQ的长; ,求sin(2α+β)的值.
,求sin(2α+β)的值.