Question

如图1-1-22,已知以梯形ABCD的对角线AC及腰AD为邻边作ACED,DC的延长线交BE于F.求证:EF =BF.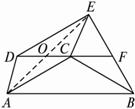

                                图1-1-22

Answer 1

思路分析:在△EAB中,OF∥AB,要说明EF=BF,只要说明O是AE的中点,而O是平行四边形对角线的交点,根据平行四边形对角线互相平分,可以知道O是AE的中点,于是问题得证.

证明:连结AE交DC于O,∵四边形ACED是平行四边形,?

∴O是AE的中点(平行四边形对角线互相平分).?

∵四边形ABCD是梯形,?

∴DC∥AB.?

在△EAB中,OF∥AB,又O是AE的中点,?

∴F是EB的中点.∴EF =BF.