题目内容
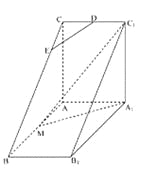
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .直角梯形
.直角梯形![]() 可以通过直角梯形
可以通过直角梯形![]() 以直线
以直线![]() 为轴旋转得到,且平面
为轴旋转得到,且平面![]() 平面
平面![]() .
.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2017/12/20/1842736631291904/1845869604462592/STEM/592e486e595e40bf846fae2bfa16ac59.png]
(I)求证: ![]() .
.
(II)求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
(III)设![]() 为
为![]() 的中点,
的中点, ![]() ,
, ![]() 分别为线段
分别为线段![]() ,
, ![]() 上的点(都不与点
上的点(都不与点![]() 重合).若直线
重合).若直线![]() 平面
平面![]() ,求
,求![]() 的长.
的长.
【答案】(I)见解析;(II)![]() ;(III)
;(III)![]() .
.
【解析】试题分析:(I)由面面垂直定理得![]() 面
面![]() ,由线面垂直定理即可得出
,由线面垂直定理即可得出![]() .
.
(II)以A为原点建立空间直角坐标系,设平面![]() 的一个法向量为
的一个法向量为![]() ,令
,令![]() ,
, ![]() ,即可求出直线
,即可求出直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
(III)设![]() ,由
,由![]() ,表示
,表示![]() ,
, ![]() ,
,
由![]() ,,求得
,,求得![]() ,,即可求出MH的长.
,,即可求出MH的长.
试题解析:(I)∵![]() ,
,
∴![]() ,
,
∵平面![]() 平面
平面![]() 且平面
且平面![]() 平面
平面![]() ,
,
∴![]() 面
面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
(II)由(I)知, ![]() 平面
平面![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() ,
,
![]() ,
, ![]() ,
, ![]() 两两垂直,
两两垂直,
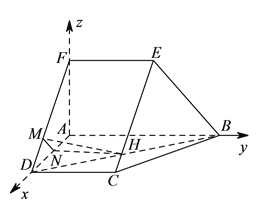
如图,以![]() 为原点建立空间直角坐标系,
为原点建立空间直角坐标系,
∵![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴![]() ,
,
∴![]() ,
,
令![]() ,
, ![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
∵![]() ,
,
![]() ,
,
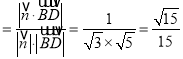 .
.
(III)在以![]() 为原点的空间直角坐标系中,
为原点的空间直角坐标系中,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
设![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
若![]() 平面
平面![]() ,
,
则![]() ,即
,即![]() ,
,
![]() ,解得
,解得![]() ,
,
∴![]() ,
,
![]() .
.
点睛:高考对空间向量与立体几何的考查主要体现在以下几个方面:①求异面直线所成的角,关键是转化为两直线的方向向量的夹角;②求直线与平面所成的角,关键是转化为直线的方向向量和平面的法向量的夹角;③求二面角,关键是转化为两平面的法向量的夹角.建立空间直角坐标系和表示出所需点的坐标是解题的关键.

 53随堂测系列答案
53随堂测系列答案【题目】甲、乙两人进行射击比赛,各射击![]() 局,每局射击
局,每局射击![]() 次,射击命中目标得
次,射击命中目标得![]() 分,未命中目标得
分,未命中目标得![]() 分,两人
分,两人![]() 局的得分情况如下:
局的得分情况如下:
甲 |
|
|
|
|
乙 |
|
|
|
|
(Ⅰ)若从甲的![]() 局比赛中,随机选取
局比赛中,随机选取![]() 局,求这
局,求这![]() 局的得分恰好相等的概率.
局的得分恰好相等的概率.
(Ⅱ)如果![]() ,从甲、乙两人的
,从甲、乙两人的![]() 局比赛中随机各选取
局比赛中随机各选取![]() 局,记这
局,记这![]() 局的得分和为
局的得分和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
(Ⅲ)在![]() 局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出
局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出![]() 的所有可能取值.(结论不要求证明)
的所有可能取值.(结论不要求证明)