题目内容
19.若sin(θ+60°)=3cos(90°-θ),则$\frac{tanθ}{tan2θ}$=$\frac{11}{25}$.分析 由题意和三角函数公式可得tanθ,再由二倍角的正切公式化简要求的式子,代值计算可得.
解答 解:∵sin(θ+60°)=3cos(90°-θ),
∴$\frac{1}{2}$sinθ+$\frac{\sqrt{3}}{2}$cosθ=3sinθ,即$\frac{\sqrt{3}}{2}$cosθ=$\frac{5}{2}$sinθ,
∴tanθ=$\frac{sinθ}{cosθ}$=$\frac{\sqrt{3}}{5}$,
∴$\frac{tanθ}{tan2θ}$=$\frac{tanθ}{\frac{2tanθ}{1-ta{n}^{2}θ}}$=$\frac{1}{2}$(1-tan2θ)=$\frac{11}{25}$,
故答案为:$\frac{11}{25}$.
点评 本题考查二倍角的正切公式,涉及同角三角函数基本关系,属基础题.

练习册系列答案
相关题目
7.已知f(x)=sinx+cosx+|sinx-cosx|,则f(x)的最小正周期为( )
| A. | 4π | B. | 2π | C. | π | D. | $\frac{π}{2}$ |
4.设等比数列{an}的前n项和为Sn,若8a2+a5=0,则下列式子中数值不能确定的是( )
| A. | $\frac{{a}_{5}}{{a}_{2}}$ | B. | $\frac{{S}_{5}}{{S}_{3}}$ | C. | $\frac{{a}_{n+1}}{{a}_{n}}$ | D. | $\frac{{S}_{n+1}}{{S}_{n}}$ |
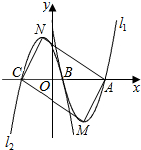 如图,己知抛物线11:y=x2-8x+12与x轴分别交于A、B两点,顶点为M.将抛物线11关于x轴作轴对称变换后再向左平移得到抛物线12,若抛物线12过点B,与x轴的另一个交点为C,顶点为N,则四边形AMCN的面积为32.
如图,己知抛物线11:y=x2-8x+12与x轴分别交于A、B两点,顶点为M.将抛物线11关于x轴作轴对称变换后再向左平移得到抛物线12,若抛物线12过点B,与x轴的另一个交点为C,顶点为N,则四边形AMCN的面积为32.