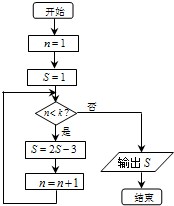
题目内容
7.某同学用“五点法”画函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$)在某一个周期内的图象时,列表并填入的部分数据如表:| x | x1 | $\frac{1}{3}$ | x2 | $\frac{7}{3}$ | x3 |
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| Asin(ωx+φ)+B | 0 | $\sqrt{3}$ | 0 | -$\sqrt{3}$ | 0 |
(Ⅱ)将f(x)的图象向右平移$\frac{2}{3}$个单位得到函数g(x)的图象,若函数g(x)在区间[0,m](3<m<4)上的图象的最高点和最低点分别为M,N,求向量$\overrightarrow{NM}$与$\overrightarrow{ON}$夹角θ的大小.
分析 (Ⅰ)由条件知,$\frac{1}{3}ω+ϕ=\frac{π}{2}$,$\frac{7}{3}ω+ϕ=\frac{3π}{2}$,从而解得ω,φ,即可解得表中的x1,x2,x3的值及函数f(x)的解析式
(Ⅱ)由函数y=Asin(ωx+φ)的图象变换规律可得g(x)解析式,由题意可求最高点为$M({1,\sqrt{3}})$,最低点为$N({3,-\sqrt{3}})$,解得$\overrightarrow{ON}=({3,-\sqrt{3}})$,$\overrightarrow{NM}=({-2,2\sqrt{3}})$,由向量的夹角公式结合角的范围即可得解.
解答 解:(Ⅰ)由条件知,$\frac{1}{3}ω+ϕ=\frac{π}{2}$,$\frac{7}{3}ω+ϕ=\frac{3π}{2}$,
∴$ω=\frac{π}{2}$,$ϕ=\frac{π}{3}$,
∴${x_1}=-\frac{2}{3},{x_2}=\frac{4}{3},{x_3}=\frac{10}{3}$,$f(x)=\sqrt{3}sin(\frac{π}{2}x+\frac{π}{3})$.
(Ⅱ)∵函数f(x)的图象向右平移$\frac{2}{3}$个单位得到函数g(x)的图象,
∴$g(x)=\sqrt{3}sin[\frac{π}{2}(x-\frac{2}{3})+\frac{π}{3}]=\sqrt{3}sin\frac{π}{2}x$,
∵函数g(x)在区间[0,m](m∈(3,4))上的图象的最高点和最低点分别为M,N,
∴最高点为$M({1,\sqrt{3}})$,最低点为$N({3,-\sqrt{3}})$,∴$\overrightarrow{ON}=({3,-\sqrt{3}})$,$\overrightarrow{NM}=({-2,2\sqrt{3}})$,
∴$cosθ=\frac{{\overrightarrow{ON}•\overrightarrow{NM}}}{{|{\overrightarrow{ON}}|•|{\overrightarrow{NM}}|}}=-\frac{{\sqrt{3}}}{2}$,又0≤θ≤π,∴$θ=\frac{5π}{6}$.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换,向量夹角公式的应用,属于基本知识的考查.

 阅读快车系列答案
阅读快车系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 2x-3y-9=0 | B. | 3x-2y-11=0 | C. | 3x+2y-7=0 | D. | x-y-5=0 |
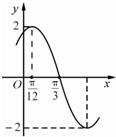 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)图象的一部分.