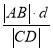题目内容
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点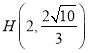 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆的方程;
(Ⅱ)点![]() 在圆
在圆![]() 上,且
上,且![]() 在第一象限,过
在第一象限,过![]() 作
作![]() 的切线交椭圆于
的切线交椭圆于![]() 两点,问:
两点,问: ![]() 的周长是否为定值?若是,求出定值;若不是,说明理由.
的周长是否为定值?若是,求出定值;若不是,说明理由.
【答案】(1)![]() ;(2)详见解析
;(2)详见解析
【解析】试题分析:(1)要求椭圆标准方程,就是要确定![]() 的值,题中焦点说明
的值,题中焦点说明![]() ,点
,点![]() 在椭圆上,把
在椭圆上,把![]() 坐标代入标准方程可得
坐标代入标准方程可得![]() 的一个方程,联立后结合
的一个方程,联立后结合![]() 可解得
可解得![]() ;(2)定值问题,就是让切线绕圆旋转,求出
;(2)定值问题,就是让切线绕圆旋转,求出![]() 的周长,为此设直线
的周长,为此设直线![]() 的方程为
的方程为![]() (
(![]() ,由它与圆相切可得
,由它与圆相切可得![]() 的关系,
的关系, ![]() ,下面来求周长,设
,下面来求周长,设![]() ,把直线方程与椭圆方程联立方程组,消元后得一元二次方程,可得
,把直线方程与椭圆方程联立方程组,消元后得一元二次方程,可得![]() ,由弦长公式
,由弦长公式![]() 得弦长,再求得
得弦长,再求得![]() (这也可由焦半径公式可得),再求周长
(这也可由焦半径公式可得),再求周长![]() ,可得定值.
,可得定值.
试题解析:(1)由题意得
所以椭圆方程为![]()
(2)由题意,设![]() 的方程为
的方程为![]()
![]() 与圆
与圆![]() 相切,
相切, ![]() ,即
,即![]()
由
设![]() ,则
,则![]()
![]()

又
![]() ,同理
,同理![]()
![]()
![]() (定值)
(定值)

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案【题目】某校学生会开展了一次关于“垃圾分类”问卷调查的实践活动,组织部分学生干部在几个大型小区随机抽取了共50名居民进行问卷调查.调查结束后,学生会对问卷结果进行了统计,并将其中一个问题“是否知道垃圾分类方法(知道或不知道)”的调查结果统计如下表:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
| 14 | 12 | 8 | 6 |
知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |
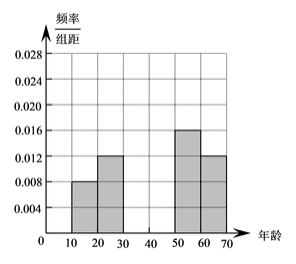
(1)求上表中的![]() 的值,并补全右图所示的的频率直方图;
的值,并补全右图所示的的频率直方图;
(2)在被调查的居民中,若从年龄在![]() 的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率
的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率
【题目】一项针对某一线城市30~50岁都市中年人的消费水平进行调查,现抽查500名(200名女性,300名男性)此城市中年人,最近一年内购买六类高价商品(电子产品、服装、手表、运动与户外用品、珠宝首饰、箱包)的金额(万元)的频数分布表如下:
女性 | 金额 |
|
|
|
|
|
频数 | 20 | 40 | 80 | 50 | 10 | |
男性 | 金额 |
|
|
|
|
|
频数 | 45 | 75 | 90 | 60 | 30 |
(1)将频率视为概率,估计该城市中年人购买六类高价商品的金额不低于5000元的概率.
(2)把购买六类高价商品的金额不低于5000元的中年人称为“高收入人群”,根据已知条件完成![]() 列联表,并据此判断能否有95%的把握认为“高收入人群”与性别有关?
列联表,并据此判断能否有95%的把握认为“高收入人群”与性别有关?
高收入人群 | 非高收入人群 | 合计 | |
女性 | 60 | ||
男性 | 180 | ||
合计 | 500 |
参考公式: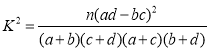 ,其中
,其中![]()
参考附表:
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |