题目内容
【题目】已知椭圆![]() 上一点
上一点![]() 关于原点的对称点为
关于原点的对称点为![]() ,
,![]() 为其右焦点,若
为其右焦点,若![]() ,设
,设![]() ,且
,且![]() ,则该椭圆的离心率
,则该椭圆的离心率![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】B
【解析】
椭圆![]() =1(a>b>0)焦点在x轴上,四边形AFF1B为长方形.根据椭圆的定义:
=1(a>b>0)焦点在x轴上,四边形AFF1B为长方形.根据椭圆的定义:
|AF|+|AF1|=2a,∠ABF=α,则∠AF1F=α.椭圆的离心率e=![]() =
=![]() =
=![]() ,α∈[
,α∈[![]() ,
,
![]() ],
],![]() ≤sin(α+
≤sin(α+![]() )≤1,
)≤1,![]() ≤
≤![]() ≤
≤![]() ﹣1,即可求得椭圆离心率e的取值范围.
﹣1,即可求得椭圆离心率e的取值范围.
椭圆![]() =1(a>b>0)焦点在x轴上,
=1(a>b>0)焦点在x轴上,
椭圆上点A关于原点的对称点为点B,F为其右焦点,设左焦点为F1,连接AF,AF1,BF,
BF1,
∴四边形AFF1B为长方形.
根据椭圆的定义:|AF|+|AF1|=2a,
∠ABF=α,则:∠AF1F=α.
∴2a=2ccosα+2csinα
椭圆的离心率e=![]() =
=![]() =
=![]() ,α∈[
,α∈[![]() ,
,![]() ],
],
∴![]() ≤α+
≤α+![]() ≤
≤![]() ,
,
则:![]() ≤sin(α+
≤sin(α+![]() )≤1,
)≤1,
∴![]() ≤
≤![]() ≤
≤![]() ﹣1,
﹣1,
∴椭圆离心率e的取值范围:![]() ,
,
故答案为:![]()

【题目】新型冠状病毒肺炎疫情爆发以来,疫情防控牵挂着所有人的心. 某市积极响应上级部门的号召,通过沿街电子屏、微信公众号等各种渠道对此战“疫”进行了持续、深入的悬窗,帮助全体市民深入了解新冠状病毒,增强战胜疫情的信心. 为了检验大家对新冠状病毒及防控知识的了解程度,该市推出了相关的知识问卷,随机抽取了年龄在15~75岁之间的200人进行调查,并按年龄绘制频率分布直方图如图所示,把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年人”和“中老年人”. 经统计“青少年人”和“中老年人”的人数比为19:21. 其中“青少年人”中有40人对防控的相关知识了解全面,“中老年人”中对防控的相关知识了解全面和不够全面的人数之比是2:1.
内的人分别称为“青少年人”和“中老年人”. 经统计“青少年人”和“中老年人”的人数比为19:21. 其中“青少年人”中有40人对防控的相关知识了解全面,“中老年人”中对防控的相关知识了解全面和不够全面的人数之比是2:1.
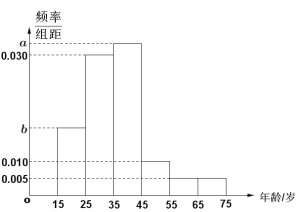
(1)求图中![]() 的值;
的值;
(2)现采取分层抽样在![]() 和
和![]() 中随机抽取8名市民,从8人中任选2人,求2人中至少有1人是“中老年人”的概率是多少?
中随机抽取8名市民,从8人中任选2人,求2人中至少有1人是“中老年人”的概率是多少?
(3)根据已知条件,完成下面的2×2列联表,并根据统计结果判断:能够有99.9%的把握认为“中老年人”比“青少年人”更加了解防控的相关知识?
了解全面 | 了解不全面 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
附表及公式: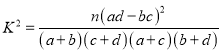 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

