题目内容
(12分)已知数列![]() 的前
的前![]() 和为
和为![]() ,其中
,其中![]() 且
且![]()
(1) 求![]() ;
;
(2)猜想数列![]() 的通项公式,并用数学归纳法加以证明。
的通项公式,并用数学归纳法加以证明。
解:(1)![]() a
a![]() =
=![]() 且a
且a![]() =
=![]()
![]() S
S![]() =n(2n-1)a
=n(2n-1)a![]()
![]() 当n=2时,
当n=2时,![]() +
+![]() ,
,![]()
当n=3时,![]() ,
,![]()
(2) 猜想:![]()
证明:i) 当n=1时,![]() 成立
成立
ii)假设当n=k(![]() )时,
)时,![]() 成立,
成立,
那么当n=k+1时 ,S![]() =(k+1)
=(k+1)![]()
![]()
S![]() =k(2k-1)
=k(2k-1)![]()
两式相减得:![]()
![]()
![]()
![]()
![]() 成立
成立
由i)、 ii)可知![]() 对于n
对于n![]() 都成立。
都成立。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列 的通项公式
的通项公式 ,设其前n项和为
,设其前n项和为 ,则使
,则使 成立的自然
成立的自然
数 有 ( )
有 ( )
| A.最大值15 | B.最小值15 | C.最大值16 | D.最小值16 |
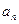 的各项均为正数,
的各项均为正数,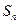 为其前n项和,对于任意的
为其前n项和,对于任意的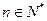 ,满足关系式
,满足关系式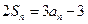
 的通项公式;
的通项公式; 的通项公式是
的通项公式是 ,求
,求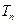 .
. 的前n项和为Sn是关于正自然数n的二次函数,其图象上有三个点A、B、C求数列
的前n项和为Sn是关于正自然数n的二次函数,其图象上有三个点A、B、C求数列
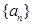 的前
的前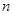 项和为
项和为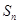 ,点
,点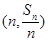 在直线
在直线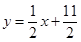 上.数列
上.数列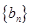 满足
满足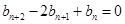
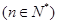 ,
,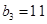 ,且其前9项和为153.
,且其前9项和为153.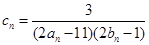 ,数列
,数列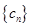 的前
的前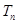 ,求使不等式
,求使不等式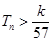 对一切
对一切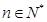 都成立的最大正整数
都成立的最大正整数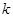 的值.
的值.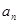 的各项均为正数,
的各项均为正数, 为其前n项和,对于任意的
为其前n项和,对于任意的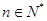 ,满足关系式
,满足关系式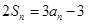
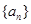 的通项公式;
的通项公式;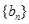 的通项公式是
的通项公式是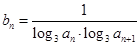 ,求
,求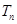 .
.