题目内容
曲线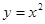 在
在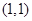 处的切线方程是( )
处的切线方程是( )
A.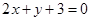 | B.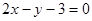 | C.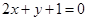 | D.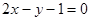 |
D
解析试题分析:因为 ,故所求切线的斜率
,故所求切线的斜率 ,所以曲线
,所以曲线 在
在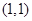 处的切线方程为
处的切线方程为 即
即 ,选D.
,选D.
考点:导数的几何意义.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
已知直线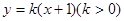 与函数
与函数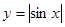 的图象恰有四个公共点
的图象恰有四个公共点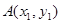 ,
,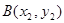 ,
,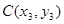 ,
,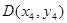 其中
其中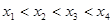 ,则有( )
,则有( )
A.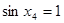 | B.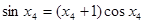 |
C.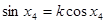 | D. |
已知函数f(x)在R上满足f(x)=2f(2-x)-x2+8x-8,则曲线y=f(x)在点(1,f(1))处的切线方程是( )
| A.y=2x-1 | B.y=x | C.y=3x-2 | D.y=-2x+3 |
设点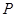 在曲线
在曲线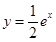 上,点
上,点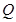 在曲线
在曲线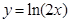 上,则
上,则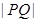 的最小值为( )
的最小值为( )
A.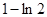 | B.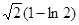 | C.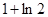 | D.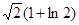 |
 与
与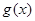 是定义在
是定义在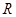 上的两个可导函数,若
上的两个可导函数,若 ,
,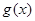 满足
满足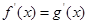 ,则
,则 与
与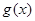 满足
满足
A.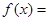 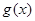 | B.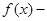 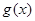 为常数函数 为常数函数 |
C.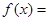 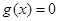 | D.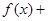 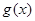 为常数函数 为常数函数 |
若 ,则
,则 ( )
( )
A. | B. | C. | D. |
函数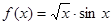 的导数为( )
的导数为( )
A.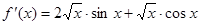 | B. |
C.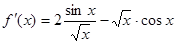 | D. |
已知曲线y=x4+ax2+1在点(-1,a+2)处切线的斜率为8,则a等于( )
| A.9 | B.6 | C.-9 | D.-6 |
一物体的运动方程为s=3+t2,则在时间段[2,2.1]内相应的平均速度为( ).
| A.4.11 | B.4.01 |
| C.4.0 | D.4.1 |