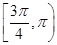题目内容
 与
与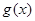 是定义在
是定义在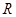 上的两个可导函数,若
上的两个可导函数,若 ,
,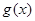 满足
满足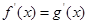 ,则
,则 与
与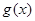 满足
满足
A.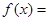 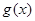 | B.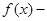 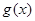 为常数函数 为常数函数 |
C.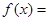 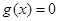 | D.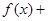 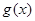 为常数函数 为常数函数 |
B
解析试题分析:由 与
与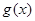 在
在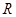 上可导,且
上可导,且 ,
,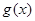 满足
满足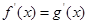 ,故
,故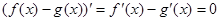 所以
所以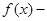
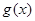 为常数函数
为常数函数
考点:可导函数的四则运算,常函数的导数

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
设函数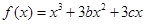 有两个极值点
有两个极值点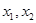 ,且
,且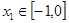 ,
,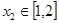 ,则( )
,则( )
A. | B.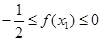 |
C. | D.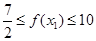 |
设函数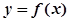 在
在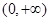 内有定义,对于给定的正数
内有定义,对于给定的正数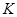 ,定义函数
,定义函数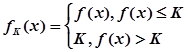 ,取函数
,取函数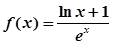 ,恒有
,恒有 ,则( )
,则( )
A.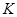 的最大值为 的最大值为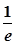 | B.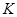 的最小值为 的最小值为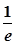 | C.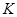 的最大值为2 的最大值为2 | D.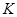 的最小值为2 的最小值为2 |
设曲线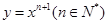 在点(1,1)处的切线与
在点(1,1)处的切线与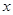 轴的交点的横坐标为
轴的交点的横坐标为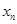 ,则
,则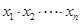 的值为
的值为
A.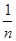 | B.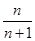 | C.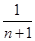 | D.1 |
函数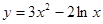 的单调增区间为( )
的单调增区间为( )
A.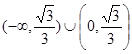 | B.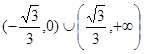 |
C.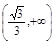 | D.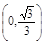 |
曲线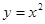 在
在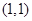 处的切线方程是( )
处的切线方程是( )
A.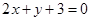 | B.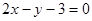 | C.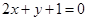 | D.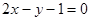 |
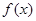 与
与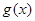 是定义在
是定义在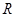 上的两个可导函数,若
上的两个可导函数,若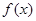 ,
,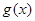 满足
满足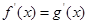 ,则
,则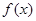 与
与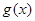 满足( )
满足( )
A.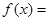 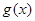 | B.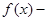 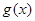 为常数函数 为常数函数 |
C.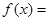 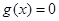 | D.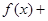 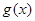 为常数函数 为常数函数 |
已知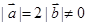 ,且关于
,且关于 的函数
的函数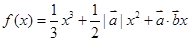 在
在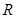 上有极值,则向量
上有极值,则向量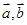 的夹角范围是( )
的夹角范围是( )
A.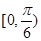 | B.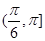 | C.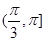 | D.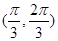 |
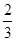 上移动,设点P处切线的倾斜角为α,则角α的取值范围是 ( ).
上移动,设点P处切线的倾斜角为α,则角α的取值范围是 ( ).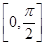
 ∪
∪