题目内容
（2013•浙江）△ABC中，∠C=90°，M是BC的中点，若sin∠BAM=
，则sin∠BAC=
．
| 1 |
| 3 |
| ||
| 3 |
| ||
| 3 |
分析：作出图象，设出未知量，在△ABM中，由正弦定理可得sin∠AMB=
，进而可得cosβ=
，在RT△ACM中，还可得cosβ=
，建立等式后可得a=
b，再由勾股定理可得c=
b，而sin∠BAC═
=
，代入化简可得答案．
| 2c |
| 3a |
| 2c |
| 3a |
| b | ||||
|
| 2 |
| 3 |
| BC |
| AB |
| a |
| c |
解答：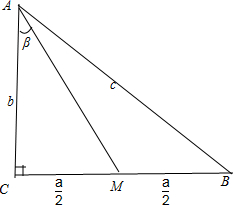
解：如图
设AC=b，AB=c，CM=MB=
，∠MAC=β，
在△ABM中，由正弦定理可得
=
，
代入数据可得
=
，解得sin∠AMB=
，
故cosβ=cos（
-∠AMC）=sin∠AMC=sin（π-∠AMB）=sin∠AMB=
，
而在RT△ACM中，cosβ=
=
，
故可得
=
，化简可得a4-4a2b2+4b4=（a2-2b2）2=0，
解之可得a=
b，再由勾股定理可得a2+b2=c2，联立可得c=
b，
故在RT△ABC中，sin∠BAC=
=
=
=
，
故答案为：
解：如图设AC=b，AB=c，CM=MB=
| a |
| 2 |
在△ABM中，由正弦定理可得
| ||
| sin∠BAM |
| c |
| sin∠AMB |
代入数据可得
| ||
|
| c |
| sin∠AMB |
| 2c |
| 3a |
故cosβ=cos（
| π |
| 2 |
| 2c |
| 3a |
而在RT△ACM中，cosβ=
| AC |
| AM |
| b | ||||
|
故可得
| b | ||||
|
| 2c |
| 3a |
解之可得a=
| 2 |
| 3 |
故在RT△ABC中，sin∠BAC=
| BC |
| AB |
| a |
| c |
| ||
|
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查正弦定理的应用，涉及三角函数的诱导公式以及勾股定理的应用，属中档题．
练习册系列答案
全优点练单元计划系列答案
相关题目