题目内容
5.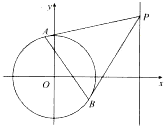 已知圆C的圆心为原点O,且与直线$x+y+4\sqrt{3}=0$相切.
已知圆C的圆心为原点O,且与直线$x+y+4\sqrt{3}=0$相切.(1)求圆C的方程;
(2)点P在直线x=8上,过P点引圆C的两条切线PA、PB,切点为A、B,试问,直线AB是否过定点,若过定点,请求出;若不过定点,请说明理由.
分析 (1)由圆C与直线相切,得到圆心到直线的距离d=r,故利用点到直线的距离公式求出d的值,即为圆C的半径,又圆心为原点,写出圆C的方程即可;
(2)由PA,PB为圆O的两条切线,根据切线的性质得到OA与AP垂直,OB与PB垂直,根据90°圆周角所对的弦为直径可得A,B在以OP为直径的圆上,设出P的坐标为(8,b),由P和O的坐标,利用线段中点坐标公式求出OP中点坐标,即为以OP为直径的圆的圆心坐标,利用两点间的距离公式求出OP的长,即为半径,写出以OP为直径的圆方程,整理后,由AB为两圆的公共弦,两圆方程相减消去平方项,得到弦AB所在直线的方程,可得出此直线方程过(3,0),得证.
解答 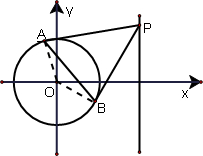 解:(1)依题意得:圆心(0,0)到直线$x+y+4\sqrt{3}=0$的距离d=r,
解:(1)依题意得:圆心(0,0)到直线$x+y+4\sqrt{3}=0$的距离d=r,
∴r=d=$\frac{4\sqrt{3}}{\sqrt{2}}$=2$\sqrt{6}$,---(2分)
∴圆C的方程为x2+y2=24①;-----(4分)
(2)连接OA,OB,
∵PA,PB是圆C的两条切线,
∴OA⊥AP,OB⊥BP,------(5分)
∴A,B在以OP为直径的圆上,-------(6分)
设点P的坐标为(8,b),b∈R,
则线段OP的中点坐标为(4,$\frac{b}{2}$),------(8分)
∴以OP为直径的圆方程为(x-4)+(y-$\frac{b}{2}$)2=16+$\frac{{b}^{2}}{4}$,②-----(10分)
∵AB为两圆的公共弦,
∴①-②得:直线AB的方程为8x+by=24,b∈R,即8(x-3)+by=0,------(13分)
则直线AB恒过定点(3,0).-------(14分)
点评 此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,切线的性质,圆周角定理,线段中点坐标公式,两点间的距离公式,点到直线的距离公式,两圆公共弦的性质,以及恒过定点的直线方程,当直线与圆相切时,圆心到直线的距离等于圆的半径,即d=r,熟练掌握此性质是解本题第一问的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分敢不必要条件 |
| A. | (-1,0) | B. | (1,+∞) | C. | (-1,0)∪(1,+∞) | D. | (-1,1) |
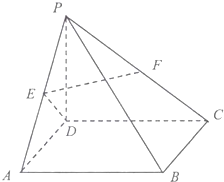 如图,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PD⊥底面ABCD,PD=DA,E、F分别为PA、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,侧棱PD⊥底面ABCD,PD=DA,E、F分别为PA、PC的中点.