题目内容
14.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>0}\\{-lo{g}_{2}(-x),x<0}\end{array}\right.$,若f(a)>f(-a),则a的取值范围是( )| A. | (-1,0) | B. | (1,+∞) | C. | (-1,0)∪(1,+∞) | D. | (-1,1) |
分析 利用分段函数,结合f(a)>f(-a),得出不等式,即可求出a的取值范围.
解答 解:由题意,a>0,则log2a>-log2a,∴a>1;
a<0,则-log2(-a)>log2(-a),∴-1<a<0,
∴a的取值范围是(-1,0)∪(1,+∞).
故选:C.
点评 本题考查分段函数,考查学生解不等式的能力,正确运用分段函数是关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
2.将甲桶中的a L水缓慢注入空桶乙中,t min后甲桶中剩余的水量符合指数衰减曲线y=aent.假设过5min后甲桶和乙桶的水量相等,若再过m min甲桶中的水只有$\frac{a}{4}$L,则m的值为( )
| A. | 5 | B. | 8 | C. | 9 | D. | 10 |
9.已知数列{an}的通项为an=log(n+1)(n+2)(n∈N*),我们把使乘积a1•a2•a3•…•an为整数的n叫做“优数”,则在(0,2015]内的所有“优数”的和为( )
| A. | 1024 | B. | 2012 | C. | 2026 | D. | 2036 |
6.已知点P(x,y)满足x2+y2≤2,则满足到直线x-y+2$\sqrt{2}$=0的距离d∈[1,3]的点P概率为( )
| A. | $\frac{1}{2}$-$\frac{1}{π}$ | B. | $\frac{1}{2}$+$\frac{1}{π}$ | C. | $\frac{1}{4}$-$\frac{1}{2π}$ | D. | $\frac{1}{4}$+$\frac{1}{2π}$ |
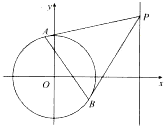 已知圆C的圆心为原点O,且与直线$x+y+4\sqrt{3}=0$相切.
已知圆C的圆心为原点O,且与直线$x+y+4\sqrt{3}=0$相切.