题目内容
9.已知抛物线y2=4x,点Q(a,0)是x轴上的一定点,过点Q作直线l与抛物线相交于A、B两点.(Ⅰ)若a=-1,点F为抛物线的焦点,且|AF|=2|BF|,求直线l的方程;
(Ⅱ)若a>0,试问在x轴上是否存在定点P,使得当直线l变动时,总有∠OPA=∠OPB(O为坐标原点)?若存在,求出点P的坐标,否则,说明理由.
分析 (Ⅰ)过A、B作准线的垂线,垂足分别为A1,B1,求出B的坐标,即可求直线l的方程.
(Ⅱ)将x=ty+a代入C得方程整理得y2-4ty-4a=0,当b=-a时,有k1+k2=0,则直线PA的倾斜角与直线PB的倾斜角互补,故∠OPA=∠OPB.
解答 解:(Ⅰ)过A、B作准线的垂线,垂足分别为A1,B1,
由|AF|=2|BF|可得|AA1|=2|BB1|,则点B为QA的中点,
连接OB,故2|OB|=|FA|.
∴|OB|=|FB|,B点的横坐标为$\frac{1}{2}$,代抛物线的方程中得B的纵坐标为±$\sqrt{2}$,
由$B(\frac{1}{2},\;±\sqrt{2})$和P(-1,0)知直线的方程为$y=±\frac{{2\sqrt{2}}}{3}(x+1)$
此时该直线与抛物线有两个交点,符合题意.-------------(6分)
(Ⅱ)存在符合题意的点P(-a,0),证明如下:
设直线l的方程为x=ty+a,
设P(b,0),A(x1,y1),B(x2,y2),直线PA,PB的斜率分别为k1,k2.
将x=ty+a代入C得方程整理得y2-4ty-4a=0.
∴y1+y2=4t,y1y2=-4a.
∴${k_1}+{k_2}=\frac{y_1}{{{x_1}-b}}+\frac{y_2}{{{x_2}-b}}$=$\frac{{2t{y_1}{y_2}+(a-b)({y_1}+{y_2})}}{{({x_1}-b)({x_2}-b)}}$=$\frac{-4t(a+b)}{{({x_1}-b)({x_2}-b)}}$.
当b=-a时,有k1+k2=0,则直线PA的倾斜角与直线PB的倾斜角互补,
故∠OPA=∠OPB,所以P(-a,0)符合题意.-------------(12分)
点评 本题考查了抛物线的标准方程及其性质、中点坐标公式、斜率计算公式,着重考查曲线方程的联立,韦达定理的使用,突出考查化归思想与方程思想,属于难题.

| A. | $±\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{4\sqrt{2}}{9}$ | D. | $\frac{7}{9}$ |
| A. | 6 | B. | 7 | C. | 10 | D. | 11 |
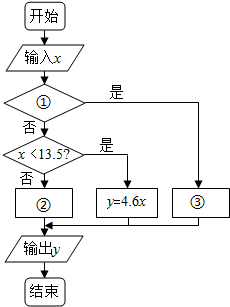 为了鼓励市民节约用水,太原市对已实施“一户一表、水表出户”的居民生活用水的收费标准规定如下:一级水量每户每月9立方米及以下,每立方米销售价格为2.30元;二级水量每户每月9立方米以上至13.5立方米,每立方米销售价格为4.60元;三级水量每户每月13.5立方米及以上,每立方米销售价格为6.90元,
为了鼓励市民节约用水,太原市对已实施“一户一表、水表出户”的居民生活用水的收费标准规定如下:一级水量每户每月9立方米及以下,每立方米销售价格为2.30元;二级水量每户每月9立方米以上至13.5立方米,每立方米销售价格为4.60元;三级水量每户每月13.5立方米及以上,每立方米销售价格为6.90元,