题目内容
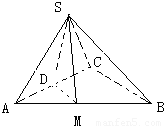
如图平面SAC⊥平面ACB,△SAC是边长为4的等边三角形,△ACB为直角三角形,∠ACB=90°,BC=4
,求二面角S-AB-C的余弦值.
| 2 |

过S点作SD⊥AC于D,过D作DM⊥AB于M,连接SM,则

∵平面SAC⊥平面ACB
∴SD⊥平面ACB
∴SM⊥AB
又∵DM⊥AB
∴∠DMS为二面角S-AB-C的平面角
在△SAC中SD=4×
=2
在△ACB中过C作CH⊥AB于H

∵AC=4,BC=4
∴AB=4
∵S=
AB•CH=
AC•BC
∴CH=
=
=
∵DM∥CH且AD=DC
∴DM=
CH=
∵SD⊥平面ACB,DM?平面ACB
∴SD⊥DM
在RT△SDM中,SM=
=
=2
,
∴cos∠DNS=
=
.

∵平面SAC⊥平面ACB
∴SD⊥平面ACB
∴SM⊥AB
又∵DM⊥AB
∴∠DMS为二面角S-AB-C的平面角
在△SAC中SD=4×
| ||
| 2 |
| 3 |
在△ACB中过C作CH⊥AB于H

∵AC=4,BC=4
| 2 |
∴AB=4
| 3 |
∵S=
| 1 |
| 2 |
| 1 |
| 2 |
∴CH=
| AC•BC |
| AB |
4•4
| ||
4
|
4
| ||
|
∵DM∥CH且AD=DC
∴DM=
| 1 |
| 2 |
2
| ||
|
∵SD⊥平面ACB,DM?平面ACB
∴SD⊥DM
在RT△SDM中,SM=
| SD2+DM2 |
(2
|
|
∴cos∠DNS=
| DM |
| SM |
| ||
| 11 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图平面SAC⊥平面ACB,△SAC是边长为4的等边三角形,△ACB为直角三角形,∠ACB=90°,BC=
如图平面SAC⊥平面ACB,△SAC是边长为4的等边三角形,△ACB为直角三角形,∠ACB=90°,BC= 如图平面SAC⊥平面ACB,ΔSAC是边长为4的等边三角形,ΔACB为直角三角形,∠ACB=90°,BC=
如图平面SAC⊥平面ACB,ΔSAC是边长为4的等边三角形,ΔACB为直角三角形,∠ACB=90°,BC= ,求二面角S-AB-C的余弦值。
,求二面角S-AB-C的余弦值。
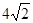 ,求二面角S-AB-C的余弦值。
,求二面角S-AB-C的余弦值。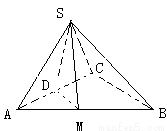
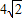 ,求二面角S-AB-C的余弦值.
,求二面角S-AB-C的余弦值.