题目内容
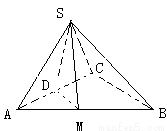
如图平面SAC⊥平面ACB,△SAC是边长为4的等边三角形,△ACB为直角三角形,∠ACB=90°,BC=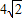 ,求二面角S-AB-C的余弦值.
,求二面角S-AB-C的余弦值.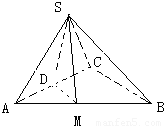
【答案】分析:过S点作SD⊥AC于D,过D作DM⊥AB于M,连接SM,则∠DMS为二面角S-AB-C的平面角,求出DM,SM,即可得出结论.
解答:解:过S点作SD⊥AC于D,过D作DM⊥AB于M,连接SM,则
∵平面SAC⊥平面ACB
∴SD⊥平面ACB
∴SM⊥AB
又∵DM⊥AB
∴∠DMS为二面角S-AB-C的平面角
在△SAC中SD=4×
在△ACB中过C作CH⊥AB于H
∵AC=4,BC=
∴AB=
∵S= AB•CH=
AB•CH= AC•BC
AC•BC
∴CH=
∵DM∥CH且AD=DC
∴DM= CH=
CH=
∵SD⊥平面ACB,DM?平面ACB
∴SD⊥DM
在RT△SDM中,SM= =
= =
= ,
,
∴cos∠DNS= =
= .
.
点评:本题考查面面角,考查学生分析解决问题的能力,正确作出面面角是关键.
解答:解:过S点作SD⊥AC于D,过D作DM⊥AB于M,连接SM,则

∵平面SAC⊥平面ACB
∴SD⊥平面ACB
∴SM⊥AB
又∵DM⊥AB
∴∠DMS为二面角S-AB-C的平面角
在△SAC中SD=4×

在△ACB中过C作CH⊥AB于H

∵AC=4,BC=

∴AB=

∵S=
 AB•CH=
AB•CH= AC•BC
AC•BC∴CH=

∵DM∥CH且AD=DC
∴DM=
 CH=
CH=
∵SD⊥平面ACB,DM?平面ACB
∴SD⊥DM
在RT△SDM中,SM=
 =
= =
= ,
,∴cos∠DNS=
 =
= .
.点评:本题考查面面角,考查学生分析解决问题的能力,正确作出面面角是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图平面SAC⊥平面ACB,△SAC是边长为4的等边三角形,△ACB为直角三角形,∠ACB=90°,BC=
如图平面SAC⊥平面ACB,△SAC是边长为4的等边三角形,△ACB为直角三角形,∠ACB=90°,BC= 如图平面SAC⊥平面ACB,ΔSAC是边长为4的等边三角形,ΔACB为直角三角形,∠ACB=90°,BC=
如图平面SAC⊥平面ACB,ΔSAC是边长为4的等边三角形,ΔACB为直角三角形,∠ACB=90°,BC= ,求二面角S-AB-C的余弦值。
,求二面角S-AB-C的余弦值。
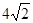 ,求二面角S-AB-C的余弦值。
,求二面角S-AB-C的余弦值。