Question

函数y=-lnx的图象与曲线y²=ex（y＞0）、直线y=0围成的面积为________．

Answer 1

分析：作出曲线y=-lnx、直线y²=ex和y=0的图象，求出它们的交点坐标．可得所求面积为函数y=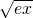在区间[0，]上的定积分，与函数y=-lnx在区间[，1]上的定积分的和．再用定积分计算公式加以运算即可得到本题答案．
解答：∵曲线y=-lnx和曲线y²=ex交点为A（，1）
曲线y=-lnx的图象与直线y=0交于点B（1，0）
∴y=-lnx的图象与曲线y²=ex（y＞0）、直线y=0围成的面积为
S=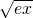dx+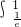（-lnx）dx
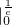=（）+[x（1-lnx）]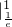
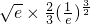=+[1×（1-ln1）-（1-ln）]
=
故答案为：
点评：本题求两条曲线围成的曲边图形的面积，着重考查了定积分的几何意义和积分计算公式等知识，属于基础题．