题目内容
已知函数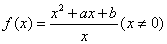 是奇函数,且满足
是奇函数,且满足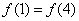
(1) 求实数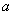 ,
,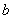 的值;
的值;
(2) 试指出函数的单调区间(不必证明),
并用定义法证明函数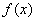 在区间
在区间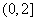 的单调性;
的单调性;
(3) 是否存在实数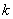 同时满足以下两个条件:
同时满足以下两个条件:
① 不等式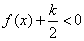 对
对 恒成立;
恒成立;
② 方程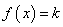 在
在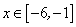 上有解.若存在,试求出实数
上有解.若存在,试求出实数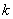 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
解:(1)由 ,解得b=4,
,解得b=4,
由 (x≠0)是奇函数,得
(x≠0)是奇函数,得 恒成立,
恒成立,
即 ;
;
(2)由(1)知, ,任取
,任取 ,
, ,
,
 ,
,
∴ ,
,
∴ ,
,
所以,函数f(x)在区间(0,2]单调递减;
类似地,可证f(x)在区间(2,+∞)单调递增。
(3)对于条件①:
由(2)可知函数f(x)在x∈(0,+∞)上有最小值
故若 对x∈(0,+∞)恒成立,
对x∈(0,+∞)恒成立,
则需 ,∴
,∴ ;
;
对于条件②:由(2)可知函数f(x)在(-∞,-2)单调递增,
在[-2,0)单调递减,
∴函数f(x)在[-6,-2]单调递增,在[-2,-1]单调递减,
又 ,
, ,
,
所以函数f(x)在[-6,-1]上的值域为 ,
,
若方程f(x)=k在[-6,-1]有解,则需 ,
,
若同时满足条件①②,则需
故当 时,条件①②同时满足.
时,条件①②同时满足.

练习册系列答案
相关题目
 …
… 的展开式中
的展开式中 的系数为________.(用数字作答)
的系数为________.(用数字作答) 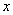 值为31,则a=__________;
值为31,则a=__________;

 ,集合
,集合 =
= ,
, =
= 。
。 ;
;

 ,满足
,满足 ,求实数
,求实数 +ln x,则 ( )
+ln x,则 ( ) 为f(x)的极大值点 B.x=
为f(x)的极大值点 B.x= 为定义在
为定义在 上的可导函数,且
上的可导函数,且 对于
对于 恒成立,则( )
恒成立,则( ) B.
B.
 D.
D.
 ,随机变量
,随机变量 的方差
的方差 ( )
( ) B.
B. C.
C. D.
D.
 所对应的边分别为
所对应的边分别为 ,若a=9,b=6, A=
,若a=9,b=6, A= ,则
,则 ( )
( ) B.
B. C.
C. D.
D.