题目内容
(12分)已知函数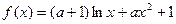
(I)讨论函数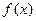 的单调性;
的单调性;
(II)设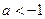 .如果对任意
.如果对任意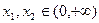 ,
,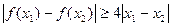 ,求
,求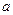 的取值范围。
的取值范围。
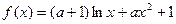
(I)讨论函数
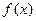 的单调性;
的单调性;(II)设
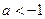 .如果对任意
.如果对任意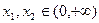 ,
,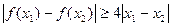 ,求
,求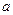 的取值范围。
的取值范围。(Ⅰ)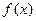 的定义域为
的定义域为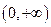 .
. 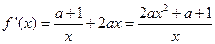 .
.
当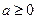 时,
时,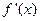 >0,故
>0,故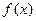 在
在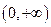 单调增加;
单调增加;
当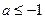 时,
时,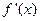 <0,故
<0,故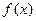 在
在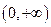 单调减少;
单调减少;
当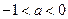 时,令
时,令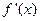 =0
=0 ,解得
,解得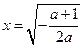 .
.
则当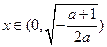 时,
时,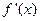 >0;
>0;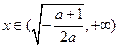 时,
时,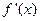 <0.
<0.
故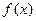 在
在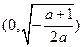 单调增加,在
单调增加,在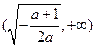 单调减少.
单调减少.
(Ⅱ)不妨假设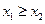 ,而
,而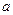 <-1,由(Ⅰ)知在
<-1,由(Ⅰ)知在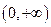 单调减少,从而
单调减少,从而
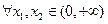 ,
,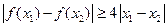
等价于
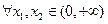 ,
,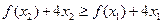 ①
①
令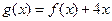 ,则
,则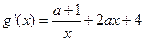
①等价于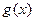 在
在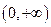 单调减少,即
单调减少,即
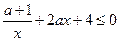 .
.
从而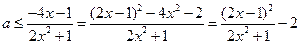
故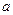 的取值范围为
的取值范围为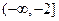 .
.
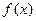 的定义域为
的定义域为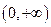 .
. 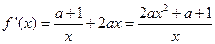 .
.当
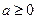 时,
时,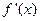 >0,故
>0,故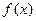 在
在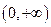 单调增加;
单调增加;当
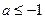 时,
时,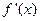 <0,故
<0,故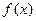 在
在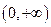 单调减少;
单调减少;当
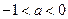 时,令
时,令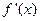 =0
=0 ,解得
,解得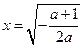 .
.则当
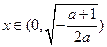 时,
时,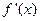 >0;
>0;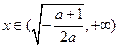 时,
时,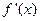 <0.
<0.故
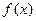 在
在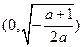 单调增加,在
单调增加,在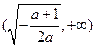 单调减少.
单调减少.(Ⅱ)不妨假设
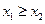 ,而
,而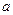 <-1,由(Ⅰ)知在
<-1,由(Ⅰ)知在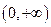 单调减少,从而
单调减少,从而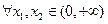 ,
,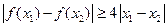
等价于
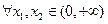 ,
,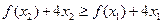 ①
①令
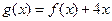 ,则
,则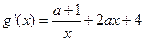
①等价于
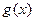 在
在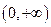 单调减少,即
单调减少,即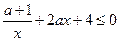 .
.从而
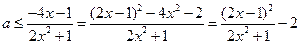
故
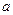 的取值范围为
的取值范围为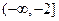 .
. 略

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
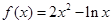 的递增区间是( ).
的递增区间是( ).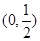

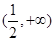
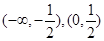
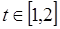 ,函数
,函数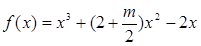 在区间
在区间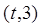 上总存在极值,求m的范围( )
上总存在极值,求m的范围( )
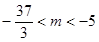
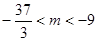
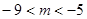
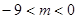
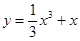 在点
在点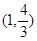 处的切线与坐标轴围成的三角形的面积为( )
处的切线与坐标轴围成的三角形的面积为( )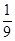

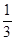
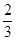
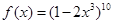 ,则
,则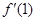 等于
等于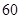
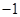
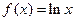
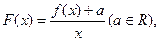 求
求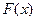 的极值;
的极值;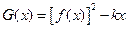 在定义域内单调递减,求满足此条件的实数
在定义域内单调递减,求满足此条件的实数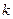 的取值范围。
的取值范围。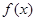 的定义域为开区间
的定义域为开区间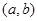 ,导函数
,导函数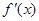 在
在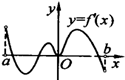
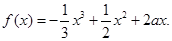
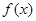 在
在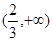 上存在单调递增区间,求
上存在单调递增区间,求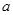 的取值范围;
的取值范围;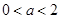 时,
时,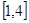 上的最小值为
上的最小值为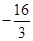 ,求
,求