题目内容
如图,在正△ABC中,点D,E分别在边AC, AB上,且AD=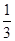 ACAE=
ACAE=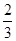 AB,BD,CE相交于点F.
AB,BD,CE相交于点F.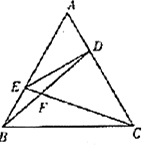
(Ⅰ)求证:A,E,F, D四点共圆;
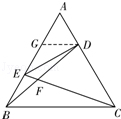
(Ⅱ)若正△ABC的边长为2,求A,E,F,D所在圆的半径.
(Ⅰ)详见解析;(Ⅱ)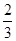 .
.
解析试题分析:(Ⅰ)根据圆内接四边形判定定理,只需说明对角互补即可,由已知数量关系,可证明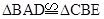 ,故
,故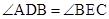 ,所以
,所以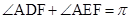 ,所以四点共圆;(Ⅱ)四边形的外接圆问题 可转化为其中三个顶点确定的外接圆问题解决,取
,所以四点共圆;(Ⅱ)四边形的外接圆问题 可转化为其中三个顶点确定的外接圆问题解决,取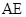 的中点
的中点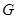 ,连接
,连接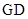 则容易证
则容易证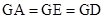
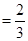 ,则
,则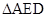 的外接圆半径为
的外接圆半径为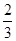 ,也是四边形的外接圆半径.
,也是四边形的外接圆半径.
试题解析:(Ⅰ)证明:∵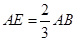 , ∴
, ∴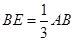 , ∵在正
, ∵在正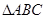 中,
中,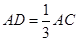 , ∴
, ∴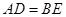 ,
,
又∵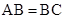 ,
,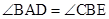 , ∴
, ∴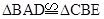 , ∴
, ∴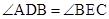 , 即
, 即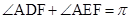 ,所以
,所以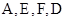 四点共圆.
四点共圆.
(Ⅱ)解:如图, 取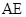 的中点
的中点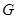 ,连接
,连接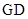 ,则
,则 , ∵
, ∵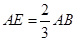 , ∴
, ∴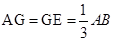 ,
, 
∵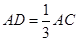 ,∴
,∴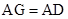 ,又
,又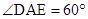 , ∴
, ∴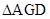 为正三角形, ∴
为正三角形, ∴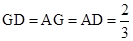 ,即
,即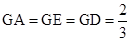 , 所以点
, 所以点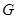 是
是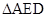 外接圆的圆心,且圆G的半径为2. 由于
外接圆的圆心,且圆G的半径为2. 由于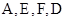 四点共圆,即
四点共圆,即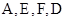 四点共圆
四点共圆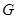 ,其半径为
,其半径为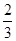 .
.
考点:1、三角形全等;2、圆内接四边形判定定理.

练习册系列答案
相关题目
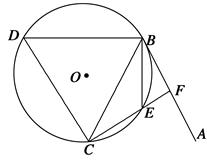
 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.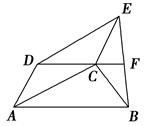
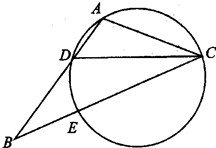
 内接于
内接于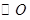 上,
上,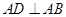 ,
,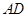 交
交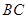 于点E,点F在DA的延长线上,
于点E,点F在DA的延长线上,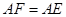 ,求证:
,求证: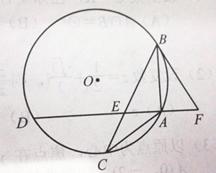
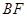 是
是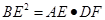 .
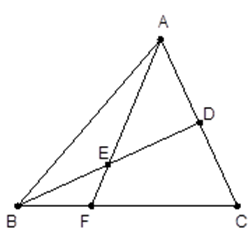
.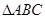 中,
中,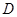 是的中点,
是的中点,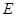 是
是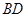 的中点,
的中点, 的延长线交
的延长线交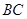 于
于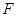 .
.
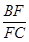 的值;
的值;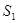 ,四边形
,四边形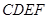 的面积为
的面积为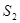 ,求
,求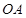 、
、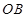 是圆
是圆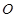 的半径,且
的半径,且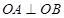 ,
,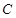 是半径
是半径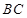 交圆
交圆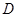 ,过
,过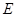 .求证:
.求证: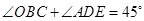 .
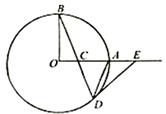
.
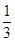 AC,AE=
AC,AE=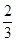 AB,BD,CE相交于点F.
AB,BD,CE相交于点F.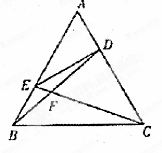
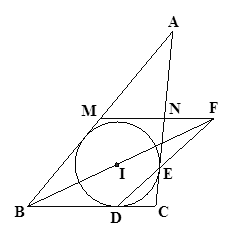
 的内心为
的内心为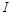 ,
,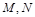 分别是
分别是 的中点,
的中点,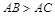 ,内切圆
,内切圆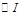 分别与边
分别与边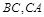 相切于
相切于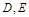 ;证明:
;证明: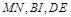 三线共点.
三线共点.