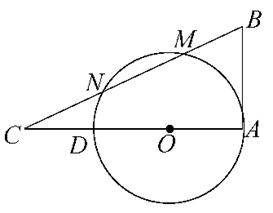
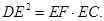题目内容
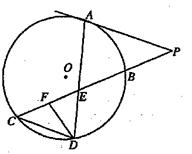
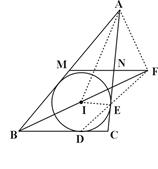
如图, 的内心为
的内心为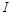 ,
,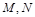 分别是
分别是 的中点,
的中点,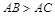 ,内切圆
,内切圆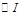 分别与边
分别与边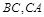 相切于
相切于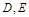 ;证明:
;证明: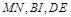 三线共点.
三线共点.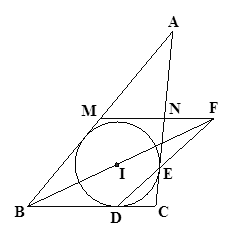
本题关键是证明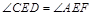
解析试题分析:先连结DE和EF,结合定理及性质得到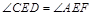 ,由此,
,由此,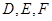 三点共线,则结论得到证明。
三点共线,则结论得到证明。
证:如图,设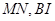 交于点
交于点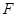 ,连
,连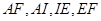 ,
,
由于中位线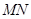 ∥
∥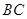 ,以及
,以及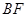 平分
平分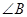 ,则
,则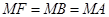 ,
,
所以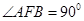 ,
,
因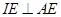 ,得
,得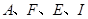 共圆.
共圆.
所以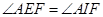 ;
;
又注意 是
是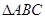 的内心,则
的内心,则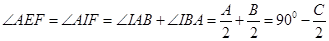 ,
,
连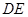 ,在
,在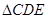 中,由于切线
中,由于切线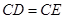 ,
,
所以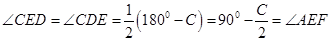 ,
,
因此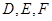 三点共线,即有
三点共线,即有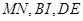 三线共点.
三线共点.
考点:几何证明
点评:本题主要考查对四点共圆的判定,三角形的内切圆与内心等知识点的理解和掌握,能熟练地运用这些知识进行推理是解此题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
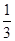 ACAE=
ACAE=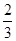 AB,BD,CE相交于点F.
AB,BD,CE相交于点F.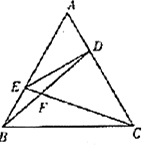
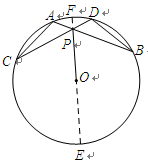
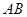 为圆
为圆 的直径,
的直径,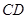 为垂直于
为垂直于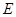 ,弦
,弦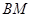 与
与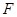 .
.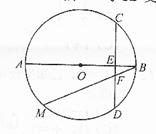
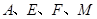 四点共圆;
四点共圆;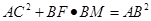 .
.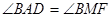 :
: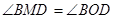 .
.
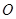 的半径为3,两条弦
的半径为3,两条弦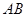 ,
,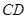 交于点
交于点 ,且
,且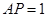 ,
, 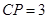 ,
,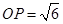 .
.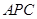 ≌△
≌△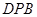 .
.