题目内容
已知等差数列{an}的公差d不为零,Sn为其前n项和,S6=5S3
(Ⅰ)求证:a2,a3,a5成等比数列;
(Ⅱ)若a2=2,且a2,a3,a5为等比数列{bn}的前三项,求数列|
|的最大项的值.
(Ⅰ)求证:a2,a3,a5成等比数列;
(Ⅱ)若a2=2,且a2,a3,a5为等比数列{bn}的前三项,求数列|
| Sn+1 |
| bn |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)利用等差数列的前n项和公式由S6=5S3,得a1=0,由此能证明a2,a3,a5成等比数列.
(Ⅱ)由已知条件得Sn=n(n-1),Sn+1=n(n+1),bn=2n,
-
=
,由此能求出数列|
|的最大项的值为
=
=
.
(Ⅱ)由已知条件得Sn=n(n-1),Sn+1=n(n+1),bn=2n,
| Sn+2 |
| 2n+1 |
| Sn+1 |
| 2n |
| (n+1)(2-n) |
| 2n+1 |
| Sn+1 |
| bn |
| S3 |
| 22 |
| 3×2 |
| 4 |
| 3 |
| 2 |
解答:
(Ⅰ)证明:∵等差数列{an}的公差d不为零,Sn为其前n项和,S6=5S3,
∴6a1+15d=15a1+15d,
解得a1=0,
∴a2=d,a3=2d,a5=4d,
∵d≠0,∴a2,a3,a5成等比数列,且公比为2.
(Ⅱ)解:∵a2=2,∴d=2,
a2,a3,a5为等比数列{bn}的前三项,
∴b1=2,b2=4,b3=8,
∴Sn=n(n-1),Sn+1=n(n+1),bn=2n,
-
=
-
=
,
当n=1时,
>
,
当n=2时,
=
,
当n≥3时,
<
,
∴
<
=
>
>…,
∴数列|
|的最大项的值为
=
=
.
∴6a1+15d=15a1+15d,
解得a1=0,
∴a2=d,a3=2d,a5=4d,
∵d≠0,∴a2,a3,a5成等比数列,且公比为2.
(Ⅱ)解:∵a2=2,∴d=2,
a2,a3,a5为等比数列{bn}的前三项,
∴b1=2,b2=4,b3=8,
∴Sn=n(n-1),Sn+1=n(n+1),bn=2n,
| Sn+2 |
| 2n+1 |
| Sn+1 |
| 2n |
| (n+1)(n+2) |
| 2n+2 |
| n(n+1) |
| 2n+1 |
| (n+1)(2-n) |
| 2n+1 |
当n=1时,
| Sn+2 |
| 2n+1 |
| Sn+1 |
| 2n |
当n=2时,
| Sn+2 |
| 2n+1 |
| Sn+1 |
| 2n |
当n≥3时,
| Sn+2 |
| 2n+1 |
| Sn+1 |
| 2n |
∴
| S2 |
| 2 |
| S3 |
| 22 |
| S4 |
| 23 |
| S5 |
| 24 |
∴数列|
| Sn+1 |
| bn |
| S3 |
| 22 |
| 3×2 |
| 4 |
| 3 |
| 2 |
点评:本题考查数列的通项公式的求法,考查数列的最大项和值的求法,是中档题,解题时要熟练掌握等差数列和等比数列的性质.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
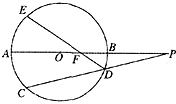 已知⊙O的半径R=2,P为直径AB延长线上一点,PB=3,割线PDC交⊙O于D,C两点,E为⊙O上一点,且
已知⊙O的半径R=2,P为直径AB延长线上一点,PB=3,割线PDC交⊙O于D,C两点,E为⊙O上一点,且