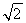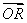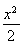题目内容
如图，直线y＝x－2与抛物线y2＝2x相交于点A，B，求证：OA⊥OB．
答案：
解析：
解析：
解法一：将y＝x－2代入y2＝2x，得
(x－2)2＝2x．
化简得x2－6x＋4＝0，
解得x＝3±
．
则y＝3±－2＝1±．
∵kOA＝
，kOB＝
，
∴kOA·kOB＝·
＝－1，
∴OA⊥OB．
解法二：同解法一得方程x2－6x＋4＝0 ①
由一元二次方程根与系数的关系，可知
x1＋x2＝6，x1·x2＝4，
∵y1＝x1－2，y2＝x2－2，
∴y1y2＝(x1－2)(x2－2)
＝x1·x2－2(x1＋x2)＋4
＝4－12＋4＝－4．
∴kOA·kOB＝
·
＝－1．
∴OA⊥OB．
练习册系列答案
相关题目
x与抛物线y＝
x2－4交于A、B两点，线段AB的垂直平分线与直线y＝－5交于Q点．
．
，判断C2与C1是否相似？如果相似，求出C2与C1的相似比；如果不相似，请说明理由；
和
分别交于点A，B和点C，D，证明：|AC|＝|BD|
判断C2与C1是否相似？如果相似，求出C2与C1的相似比；如果不相似，请说明理由；
分别交于点A，B和点C，D，试在椭圆M和椭圆Mλ上分别作出点E和点F(非椭圆顶点)，使△CDF和△ABE组成以λ为相似的两个相似三角形，写出具体作法．(不必证明)
