题目内容
已知数列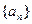 和
和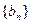 满足:
满足: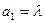 ,
,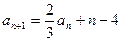 ,
,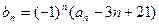 ,其中
,其中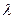 为实数,
为实数,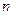 为正整数。
为正整数。
(Ⅰ)证明:对任意的实数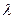 ,数列
,数列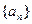 不是等比数列;
不是等比数列;
(Ⅱ)证明:当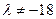 时,数列
时,数列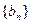 是等比数列;
是等比数列;
(Ⅲ)设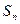 为数列
为数列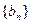 的前
的前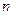 项和,是否存在实数
项和,是否存在实数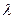 ,使得对任意正整数
,使得对任意正整数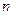 ,都有
,都有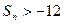 ?若存在,求
?若存在,求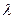 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
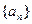 和
和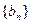 满足:
满足: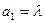 ,
,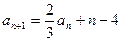 ,
,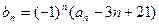 ,其中
,其中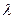 为实数,
为实数,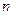 为正整数。
为正整数。(Ⅰ)证明:对任意的实数
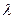 ,数列
,数列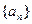 不是等比数列;
不是等比数列;(Ⅱ)证明:当
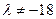 时,数列
时,数列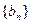 是等比数列;
是等比数列;(Ⅲ)设
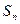 为数列
为数列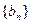 的前
的前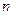 项和,是否存在实数
项和,是否存在实数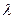 ,使得对任意正整数
,使得对任意正整数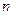 ,都有
,都有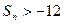 ?若存在,求
?若存在,求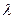 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。(Ⅰ)证明:假设存在一个实数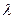 ,使
,使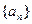 是等比数列,则有
是等比数列,则有 ,即
,即
 ,矛盾。
,矛盾。
所以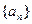 不是等比数列。
不是等比数列。
(Ⅱ)证明:
 。
。
又 。由上式知
。由上式知 ,
,
故当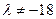 时,数列
时,数列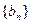 是以
是以 为首项,
为首项, 为公比的等比数列。
为公比的等比数列。
(Ⅲ)当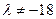 时,由(Ⅱ)得
时,由(Ⅱ)得 ,于是
,于是
 ,
,
当 时,
时, ,从而
,从而 。上式仍成立。
。上式仍成立。
要使对任意正整数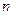 ,都有
,都有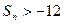 。
。
即 。
。
令 ,则
,则
当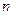 为正奇数时,
为正奇数时, :当
:当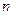 为正偶数时,
为正偶数时, ,
,
 的最大值为
的最大值为 。
。
于是可得 。
。
综上所述,存在实数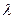 ,使得对任意正整数
,使得对任意正整数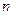 ,都有
,都有 ;
;
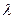 的取值范围为
的取值范围为 。
。
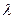 ,使
,使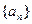 是等比数列,则有
是等比数列,则有 ,即
,即 ,矛盾。
,矛盾。所以
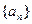 不是等比数列。
不是等比数列。(Ⅱ)证明:

 。
。又
 。由上式知
。由上式知 ,
,故当
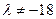 时,数列
时,数列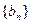 是以
是以 为首项,
为首项, 为公比的等比数列。
为公比的等比数列。(Ⅲ)当
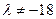 时,由(Ⅱ)得
时,由(Ⅱ)得 ,于是
,于是 ,
,当
 时,
时, ,从而
,从而 。上式仍成立。
。上式仍成立。要使对任意正整数
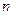 ,都有
,都有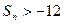 。
。即
 。
。令
 ,则
,则当
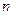 为正奇数时,
为正奇数时, :当
:当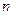 为正偶数时,
为正偶数时, ,
, 的最大值为
的最大值为 。
。于是可得
 。
。综上所述,存在实数
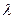 ,使得对任意正整数
,使得对任意正整数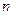 ,都有
,都有 ;
;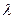 的取值范围为
的取值范围为 。
。略

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
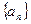 的前n项和为
的前n项和为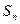 ,已知
,已知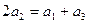 ,数
,数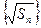 是公差为
是公差为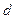 的等差数列。
的等差数列。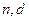 表示);
表示);
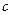 为实数,对满足
为实数,对满足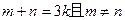 的任意正整数
的任意正整数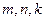 ,不等式
,不等式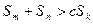 都成立。求证:
都成立。求证: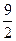 。
。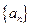 的前
的前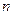 项和为
项和为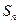 ,对任意的
,对任意的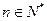 ,点
,点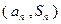 都在直线
都在直线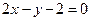 的图像上.
的图像上.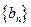 ,使得
,使得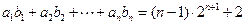 对一切
对一切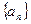 中,
中,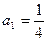 ;
;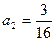 ,对任意的
,对任意的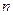 为正整数都有
为正整数都有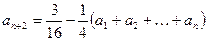 。
。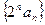 是等差数列;
是等差数列;
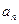 ;
;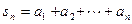 (
(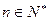 ),是否存在实数
),是否存在实数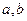 使得
使得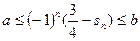 对任意的
对任意的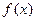 的图象经过点
的图象经过点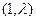 ,且对任意
,且对任意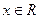 ,都有
,都有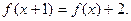 数列
数列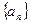 满足
满足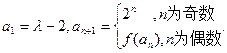
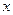 为正整数时,求
为正整数时,求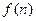 的表达式
的表达式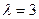 ,求
,求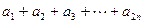
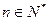 ,总有
,总有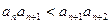 ,求实数
,求实数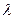 的取值范围
的取值范围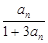 ,a1=2,则a4为 ( )
,a1=2,则a4为 ( )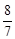
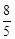
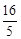
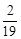
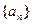 的前n项和为
的前n项和为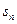 ,
,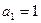 且满足
且满足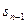 +n (n>1且n
+n (n>1且n ∈
∈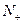 )
)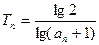 ,求使得不等式
,求使得不等式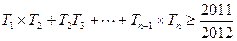 成立的最小正整数n的值
成立的最小正整数n的值 ,圆
,圆 和圆
和圆 若
若 平分
平分 的周长,则
的周长,则 的所有项和为
的所有项和为  (
( ),①如果
),①如果 ,那么
,那么 =
=

 4;
4; ,那么
,那么 =
=

 ,那么
,那么