题目内容
已知数列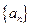 的前
的前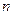 项和为
项和为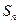 ,对任意的
,对任意的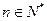 ,点
,点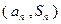 都在直线
都在直线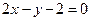 的图像上.
的图像上.
(1)求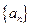 的通项公式;
的通项公式;
(2)是否存在等差数列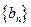 ,使得
,使得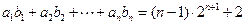 对一切
对一切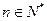 都成立?若存在,求出
都成立?若存在,求出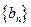 的通项公式;若不存在,说明理由.
的通项公式;若不存在,说明理由.
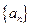 的前
的前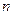 项和为
项和为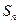 ,对任意的
,对任意的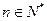 ,点
,点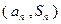 都在直线
都在直线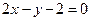 的图像上.
的图像上.(1)求
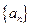 的通项公式;
的通项公式;(2)是否存在等差数列
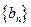 ,使得
,使得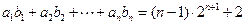 对一切
对一切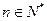 都成立?若存在,求出
都成立?若存在,求出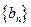 的通项公式;若不存在,说明理由.
的通项公式;若不存在,说明理由.(I)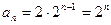 (II) 存在
(II) 存在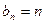 (
(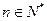 )满足条件
)满足条件
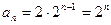 (II) 存在
(II) 存在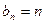 (
(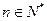 )满足条件
)满足条件(I)由题意得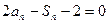 …………… ……2分
…………… ……2分
当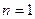 时,
时,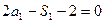 得
得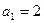
当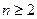 时 由
时 由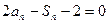 (1)得网w。w-w*k&s%5¥u
(1)得网w。w-w*k&s%5¥u
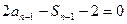 (2)
(2)
(1)-(2)得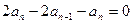 即
即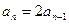 …………………4分
…………………4分
因为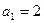 所以
所以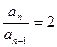 ,所以
,所以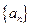 是以2为首项,2为公比的等比数列
是以2为首项,2为公比的等比数列
所以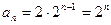 …………………6分
…………………6分
(II)假设存在等差数列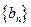 ,使得
,使得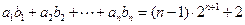 对一切
对一切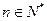 都成立
都成立
则 当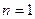 时,
时,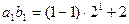 得
得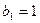 …………………8分
…………………8分
当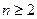 时 由
时 由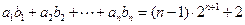 (3)得
(3)得
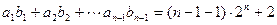 (4)
(4)
(3)-(4)得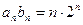 即
即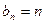 …………… …10分
…………… …10分
当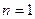 时也满足条件,所以
时也满足条件,所以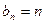 …………………11分
…………………11分
因为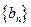 为等差数列,故存在
为等差数列,故存在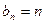 (
(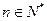 )满足条件 ………………13分
)满足条件 ………………13分
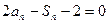 …………… ……2分
…………… ……2分当
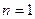 时,
时,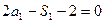 得
得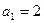
当
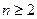 时 由
时 由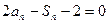 (1)得网w。w-w*k&s%5¥u
(1)得网w。w-w*k&s%5¥u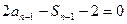 (2)
(2)(1)-(2)得
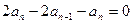 即
即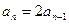 …………………4分
…………………4分因为
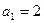 所以
所以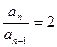 ,所以
,所以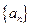 是以2为首项,2为公比的等比数列
是以2为首项,2为公比的等比数列所以
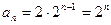 …………………6分
…………………6分(II)假设存在等差数列
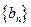 ,使得
,使得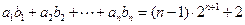 对一切
对一切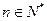 都成立
都成立则 当
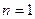 时,
时,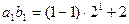 得
得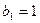 …………………8分
…………………8分当
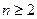 时 由
时 由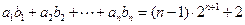 (3)得
(3)得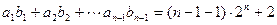 (4)
(4)(3)-(4)得
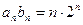 即
即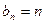 …………… …10分
…………… …10分当
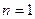 时也满足条件,所以
时也满足条件,所以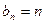 …………………11分
…………………11分因为
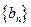 为等差数列,故存在
为等差数列,故存在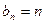 (
(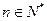 )满足条件 ………………13分
)满足条件 ………………13分
练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
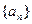 的前
的前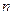 项和
项和 满足
满足
 的值; (2)求
的值; (2)求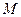 使下列不等式:
使下列不等式: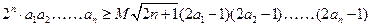
 成立?若存在,求出M的取值范围;若不存在,请说明理由
成立?若存在,求出M的取值范围;若不存在,请说明理由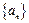 的各项均是正数,其前
的各项均是正数,其前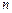 项和为
项和为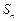 ,满足
,满足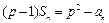 ,其中
,其中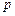 为正常数,且
为正常数,且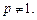
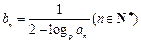 ,数列
,数列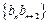 的前
的前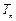 ,求证:
,求证: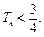
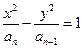 的一个焦点为(
的一个焦点为(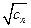 ,0),一条渐近线方程为
,0),一条渐近线方程为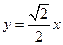 ,其中
,其中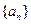
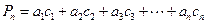 .
.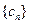 的通项公式;
的通项公式; 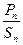 ;
;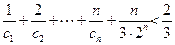 +
+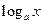 (a>0,且a≠1)对一切自然数n恒成立,求实数x的取值范围.
(a>0,且a≠1)对一切自然数n恒成立,求实数x的取值范围.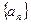 满足:
满足: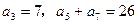 ,
,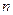 项和为
项和为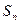 。
。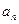 及
及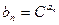 (其中
(其中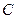 为常数,且
为常数,且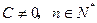 ),求证数列
),求证数列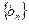 为等比数列。
为等比数列。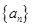 满足
满足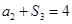 ,
,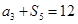 ,则
,则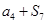 的值是( )
的值是( )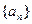 和
和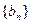 满足:
满足: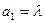 ,
,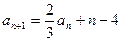 ,
,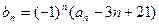 ,其中
,其中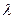 为实数,
为实数,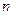 为正整数。
为正整数。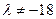 时,数列
时,数列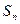 为数列
为数列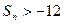 ?若存在,求
?若存在,求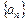 中,
中,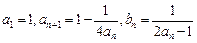 ,其中
,其中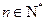 .
.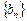 为等差数列;
为等差数列;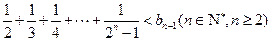
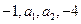 成等差数列,
成等差数列, 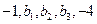 成等比数列,则
成等比数列,则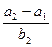 的值为________.
的值为________.