题目内容
函数y=sin(2x+
),则下列关于它的图象的说法不正确的是( )
| π |
| 3 |
A、关于点(-
| ||
B、关于点(
| ||
C、关于直线x=
| ||
D、关于直线x=
|
考点:正弦函数的对称性
专题:三角函数的图像与性质
分析:利用正弦函数的对称性,判断各个选项是否正确,从而得出结论.
解答:
解:对于函数y=sin(2x+
),当x=-
时,求得y=0,可得函数的图象关于点(-
,0)对称,故A正确.
当x=
时,求得y=0,可得函数的图象关于点(
,0)对称,故B正确.
当x=
时,求得y=-1为最大值,可得函数的图象关于直线x=
对称,故C正确.
当x=
时,求得y=-
不是最大值,可得函数的图象不关于直线x=
对称,故D不正确,
故选:D.
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
当x=
| π |
| 3 |
| π |
| 3 |
当x=
| 7π |
| 12 |
| 7π |
| 12 |
当x=
| 5π |
| 12 |
| 1 |
| 2 |
| 7π |
| 12 |
故选:D.
点评:本题主要考查正弦函数的对称性,属于基础题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知平面向量
=(1,2),
=(-3,x),若
∥
,则x等于( )
| a |
| b |
| a |
| b |
| A、2 | B、-3 | C、6 | D、-6 |
sin240°=( )
A、-
| ||||
| B、-1 | ||||
| C、-2 | ||||
| D、1 |
给出一个算法的程序框图(如图所示),该程序框图的功能是( )
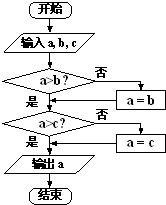

| A、求输出a,b,c三数的最大数 |
| B、求输出a,b,c三数的最小数 |
| C、将a,b,c按从小到大排列 |
| D、将a,b,c按从大到小排列 |
下列方程中,t为参数.与方程y2=x表示同一曲线的是( )
A、
| |||||||||
B、
| |||||||||
C、
| |||||||||
D、
|